Received: Aug 10, 2025 Accepted: Jan 13, 2026 Available Online: Feb 15, 2026 Published: Feb 15, 2026
DOI: 10.5937/jaes0-62039
DEVELOPMENT OF SIMILARITY CRITERIA FOR PHYSICAL MODELING OF THE PROCESS OF ROADBED COMPACTION
Abstract
This paper focuses on developing criteria for the physical modeling of roadbed compaction using a vibration roller. A rheological model of the process was employed to establish the relationship between stresses and strains in soils with elastic-viscoplastic properties. Additional similarity criteria were utilized to characterize the design and technological specifications, as well as the initial and boundary conditions of the process. Based on these similarity criteria, a physical model of the working element of a vibration roller was created. A series of experiments was conducted to identify the key parameters of this working element. By analyzing the inverse relationships that define these key design and technological parameters, it is possible to determine optimal values for the essential parameters of the vibration roller.
Highlights
- The efficiency of compacting the roadbed using vibratory rollers depends on a large number of parameters, including design and technology, as well as the properties of the soil being compacted.
- The physical modeling method used in this study made it possible to take into account the influence of a large number of factors on the process of compaction of the roadbed.
- The novelty of the study lies in the set of developed similarity criteria, taking into account all intermediate phases of the soil in which it is located during the compaction process.
- The advantage of physical modeling is that it allows for the determination of rational values for key parameters with minimal time and cost. Another advantage of this method is that the results of this study can be generalized to all similar systems.
Keywords
Content
1 Introduction
The requirements for road surfaces, such as load-bearing capacity, stability, and strength, are becoming increasingly stringent. This is largely due to factors such as the growing use of heavy vehicles and high traffic volumes, which result in greater axial loads on road surfaces. Although roadbed compaction costs represent approximately 5-7 percent of the total road construction expenses, the significance of maintaining high-quality roadbed compaction cannot be overstated.
Consequently, the quality of roadbed compaction is directly linked to the overall quality of the road structure. The primary equipment used for roadbed compaction is rollers of various types, with vibration rollers currently making up about 80 percent of all rollers in use. This is because vibration rollers can significantly enhance the force exerted on the compacted material. Additionally, the motion of eccentric rollers causes mineral grains in soil to rearrange, leading to more effective compaction.
Numerous studies are currently focused on analyzing and synthesizing the subgrade compaction processes, as well as selecting and justifying the design, technological, and geometric parameters of compaction equipment. Notable contributions from foreign researchers include works by R-Y. Zhang [1], G. Spagnoli [2], H-Ch.Dan [3], J.Pistrol [4],I.Sharonov [5],N-J.Syamini [6],Q.Zhang[7],Sh.Li [8], K.Glavatsky[9], Z.G. Ter–Martirsyan [10], S.J.Poulos [11], Kurdyumov[12], C.Dragos [13], V. Mikheyev [14]. Their research focuses on the compaction process, identifying factors that influence compaction efficiency, and justifying the key design and technological parameters of vibration rollers. However, these studies do not address the physical modeling of the roadbed compaction process using vibration rollers. Among domestic researchers, the works of T. Khankelov [15,16,17,18,19] and S. Komilov [20] are noteworthy. T. Khankelov has explored the physical modeling of trench compaction with backfill soils and has determined rational values for key parameters of segmental working bodies. S. Komilov's research primarily examines the specific features of soil compaction using vibration rollers, including how to select the appropriate type of roller based on the tasks and the properties of the soil being compacted.
Establishing relationships between stresses and strains in compacted subgrades is essential, as it determines the parameters and operating modes of compacting machines and mechanisms. Rheological models provide a clear understanding of the pattern of changes in stresses and strains in a medium, depending on variations in its defining physical and mechanical properties under mechanical stress. For this purpose, rheological models of varying structure and complexity have been developed for the process of soil compaction by wheeled propellers. The rheological model of the wheel propeller-soil system developed by Professor V.I. Balovnev [21] is presented in Fig. 1.
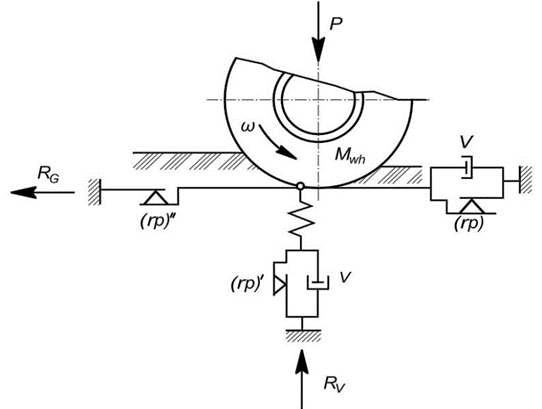
Fig. 1. Rheological model of the wheel propeller-soil system
The horizontal reactive component of the wheel ($R_G$) is simulated by the viscoplastic model ($rp$) ($v$), which represents the Bingham model without an elastic element. The vertical reaction to the wheel ($R_V$) is simulated by the elastic-viscoplastic Bingham model. The equations describing the Bingham elastoviscoplastic model are as follows:
| $tau = \eta \frac{d\vartheta}{dz} + \tau_{rp}, \quad \tau = \gamma G, \quad \tau = \gamma_1 G_1 + \tau_{rp}$ | (1) |
where $\tau$ - is the shear stress, $N/m^2$; η - is the dynamic viscosity coefficient, $Ns/m^2$; $\vartheta$ - is the velocity of displacement,$m/s$; z - is the distance, $m$; $G$ - is the shear modulus, $N/m^2$; $\gamma$ - is the shear strain, $/tau_rp$ - is the shear stress corresponding to the yield strength, $N/m^2$; $\gamma_1$, $G_1$ - are the shear strain and shear modulus for the viscoplastic zone, respectively.
Additional similarity criteria describing the subgrade compaction process are found primarily by two methods: differential equation analysis and dimensional analysis [22].
For a more in-depth analysis of the compaction process of the roadbed using a vibration roller, a rheological model developed by Professor Balovnev and a dimensional analysis method were used.
2 Materials and methods
Based on equation (1) of the rheological model of the process of compaction of the roadbed by the working element of a vibration roller, we find the primary similarity criteria by dividing all the terms of the equation by one of them. Using the integral analog method [23], we determine four criteria:
where:
- $\pi_1$ is the ratio of horizontal forces to the forces acting in the horizontal direction in the plastic zone of compaction;
- $\pi_2$ is the ratio of inertial forces to the horizontal forces acting in the plastic zone;
- $\pi_3$ is the ratio of shear forces to the forces leading to soil deformation;
- $\pi_4$ is the ratio of the shear forces to the forces causing soil deformation in the layered zone.
Additional similarity criteria for the subgrade compaction process can be identified through dimensional analysis. For this purpose, we will consider the roller-soil system. The interaction diagram between the roller drum and the subgrade is shown in Figure 2.
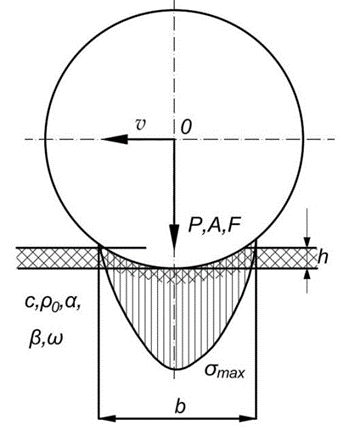
Fig. 2. Vibration roller-soil system
A vibration roller can be defined by the following parameters: diameter D, width L, and weight P. The compaction mode can be characterized by compaction depth h, amplitude A, frequency F, roller speed ϑ, and gravitational acceleration g. Soil medium is characterized by cohesion c, internal friction angle α and external friction angle β, initial density $\rho_0 $, and moisture content ω.
The soil density at a given time point is determined as:
| $\rho_n = f(D, L, P, h, A, F, \vartheta, g, c, \alpha, \beta, \rho_0, \omega)$ | (3) |
Let us establish criteria to describe the process of roadbed compaction using a vibration roller. In this case, we have 14 physical quantities characterizing the process ($n$ =13). Upon examining these quantities, we find that three of them ($\alpha, \beta, \omega$) are themselves criteria of similarity [24]. The dimensions of the remaining physical quantities, which total 14 - 3 = 11, can be expressed using three basic units of measurement: force P, length L, and time T.
Here are the formulas for the dimensions of these quantities:
| $[D] = [L] = [h] = [A] = L, [P] = P, [F] = T^-1, [c] = P L^-2, [\vartheta] = L T^-1, [g] = L T^-2, [\rho_0] = P L^-3$ | (4) |
To identify additional similarity criteria, we need to select base quantities that have independent dimensions and incorporate all the basic units of measurement. In this scenario, we will use the following three quantities with independent dimensions: $\rho_0, D, g \; (m = 3)$. Consequently, we need to derive 14 - 3 = 11 similarity criteria. For example, to find criterion $\pi_5$, we take the dimension of parameter ρ and place it in the numerator. In the denominator, we write the product of the dimensions of $\rho_0, R, g$ with the currently unknown exponents $a_1, a_2, a_3$.
$\pi_5 = \frac{P L^{-3}}{(P L^{-3})^{a_1} \, L^{a_2} \, (L T^{-2})^{a_3}}$
We determine the exponents by equating the dimensions of the numerator and denominator to obtain a dimensionless complex. Thus, for $a_1 = 1, \; a_2 = 0, \; a_3 = 0 $, we obtain:
$\pi_5 = \frac{P L^{-3}}{(P L^{-3})^1 \, L^0 \, (L T^{-2})^0} = \frac{\rho}{\rho_0}$
The remaining similarity criteria are obtained in the same way. We write out all the similarity criteria:
| $\pi_5 = \frac{\rho}{\rho_0}, \; \pi_6 = \frac{L}{D}, \; \pi_7 = \frac{h}{D}, \; \pi_8 = \frac{A}{D}, \; \pi_9 = \frac{P}{\rho_0 D^3}, \; \pi_{10} = F \sqrt{\frac{D}{g}}, \; \pi_{11} = \frac{\vartheta}{\sqrt{g D}}, \; \pi_{12} = \frac{C}{\rho_0 D}, \; \pi_{13} = \alpha, \; \pi_{14} = \beta, \; \pi_{15} = \omega$ | (5) |
where
- $\pi_5$ – is the ratio of the soil density at an arbitrary time point to the soil density at the initial time point;
- $\pi_6$ – is the ratio of the width of the vibration roller drum to its diameter;
- $\pi_7$ – is the ratio of the compaction depth to the vibration roller drum diameter;
- $\pi_8$ – is the ratio of the amplitude developed by the vibrator to the vibration roller drum diameter;
- $\pi_9$ – is the ratio of the compaction force to the volumetric forces;
- $\pi_{10}$ – is the ratio of the dynamic components of the compaction forces to the drum weight;
- $\pi_{11}$ – is the ratio of the inertial forces to the volumetric forces;
- $\pi_{12}$ – is the ratio of the cohesion forces to the volumetric forces;
- $\pi_{13}$ – is the criterion characterizing the equality of the angles of internal friction;
- $\pi_{14}$ – is the criterion characterizing the equality of the angles of external friction;
- $\pi_{15}$ – is the criterion characterizing the equality of soil moisture content values.
For easier use, we square criterion $\pi_11$:
$\pi_{11} = \frac{\vartheta^2}{g D} $
The criterion equation has the following form:
| $\pi_5 = f\left(\pi_1, \pi_2, \pi_3, \pi_4, \pi_6, \pi_7, \pi_8, \pi_9, \pi_{10}, \pi_{11}, \pi_{12}, \pi_{13}, \pi_{14}, \pi_{15}\right) $ | (6) |
Equation (5) is an implicit criteria equation. Its analytical solution presents several difficulties; more common special cases can be considered. From a priori sources [25,26, 27], it is known that the most representative soil type for the Republic of Uzbekistan is sandy loam; its moisture content during the roadbed construction fluctuates between 8 and 10%. By watering, the value is brought to approximately 18%. The internal friction angle is approximately $\alpha \approx 22^\circ$, the external friction angle is $\beta \approx 35^\circ $, and the ratio of the drum width to its diameter is $\frac{L}{D} \approx 1{,}2 \div 1{,}35 $. Then, our criteria equation is:
| $\pi_5 = f\left(\pi_8, \pi_9, \pi_{10}, \pi_{11}\right)$ | (7) |
For a given value of D, which corresponds to a specific brand of the roller, criteria $\pi_8, \pi_9, \pi_{10}, \pi_{11} $ uniquely determine parameters A, P, F, and ϑ, respectively. These parameters function as factors in the experimental studies, while the soil compaction coefficient is the output parameter.
In modeling the compaction process of the roadbed, the XS123H vibration roller model was used as an analog. A necessary condition for ensuring dynamic and kinematic similarities between the physical model and the full-scale machine used in the process of compaction of the roadbed is compliance with the following criteria:
The scales of physical quantities were determined using formulas that define similarity indices. These similarity indices were calculated by dividing the similarity criteria for the original case by the similarity criteria for the model.
For example, for criteria $\pi_9, \pi_{10}, \text{ and } \pi_{11}$, the relationship among scales $k_P, k_F $, and $k_{\vartheta} $ and other scales has the following form:
Independent scales were $k_D, k_{\rho_0}$, and$k_g$, the linear scale was $k_D=4$, since during
| $\frac{k_P}{k_{\rho_0} k_D^3} = 1, \quad \frac{k_F \sqrt{k_D}}{\sqrt{k_g}} = 1, \quad \frac{k_{\vartheta}}{\sqrt{k_g k_D}} = 1 $ | (9) |
The experimental studies, the properties of the compacted material did not change, and the experiment was carried out on the ground $k_{\rho_0} = k_g = 1 $. The experiments were carried out under conditions of approximate physical modeling, and the scale values of physical quantities were determined by the linear scale of the model:
| $k_P = k_D^3, \quad k_F = \frac{1}{\sqrt{k_D}}, \quad k_{\vartheta} = \sqrt{k_D} $ | (10) |
To achieve dynamic and kinematic similarity in the compaction processes, the chosen linear scale dictates that the model should be 64 times smaller than the original. Additionally, the compaction frequency of the physical model must be twice that of the original, while the compaction velocity of the physical model should be half that of the original. Based on the data collected to ensure geometric, dynamic, and kinematic similarity, a physical model of the vibratory roller has been developed.
To investigate the compaction patterns of a roadbed with a vibration roller, a physical model of the roller was constructed at a scale of k = 4. The developed physical model of the roller, featuring a three-point frame installed on a soil channel, is illustrated in Fig. 3.

Fig. 3. Fragment of an experiment to establish roadbed compaction patterns on a physical simulation setup
Using the methods based on mathematical statistics theory, preliminary distribution, and the results of single-factor experiments, the key factors determining the compaction process were identified. The dependence of the compaction coefficient of the machine on the main process parameters is implicitly expressed as:
| $Y = f(A, P, F, \vartheta)$ | (11) |
where $A$ is the compaction amplitude of the vibratory drum, mm; P is the compaction force, N; F is the compaction frequency of the vibratory drum, Hz; ϑ is the roller speed, m/s; Y is the compaction coefficient. To determine the variation ranges for the key factors that significantly influence soil compaction using a vibratory roller, a series of single-factor experiments was conducted. Figure 4 illustrates the relationship between soil density and moisture content.
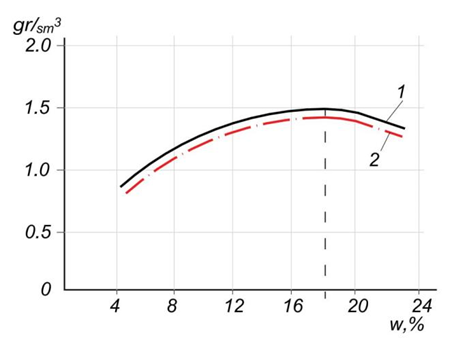
Fig. 4. Soil density versus moisture content: 1 - experimental curve; 2 - theoretical curve calculated using regression formulas
Analysis of the graphs indicates that the maximum soil density occurs at a moisture content of approximately $\omega \approx 18\%$. This is explained by the fact that at this level of moisture content, the cohesive forces between the mineral particles are at their strongest.
Figure 5 presents graphs depicting the relationship between soil density and compaction force.
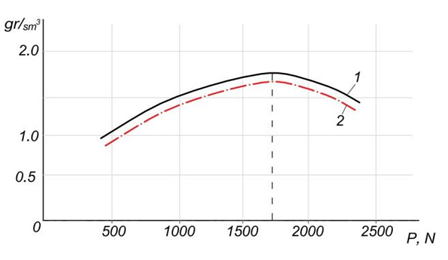
Fig. 5. Soil density versus compaction force: 1 - experimental curve; 2 - theoretical curve calculated using regression formulas
Analysis of the graphs in this figure indicates that the optimal soil density values are achieved with a compaction force of approximately $P \approx 1{,}7~\text{kN} $. This observation can be attributed to the onset of plastic soil flow when the compaction force exceeds this value.
Figure 6 displays the results of a single-factor experiment that examines how soil density correlates with the drum amplitude of a vibratory roller.
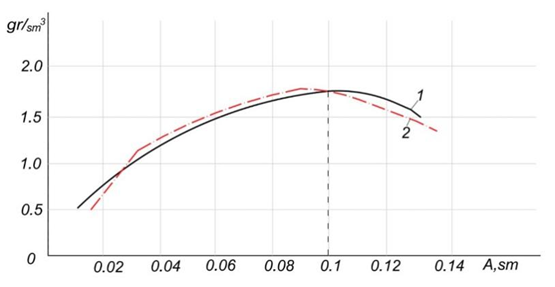
Fig. 6. Soil density versus vibratory roller drum amplitude: 1 - experimental curve; 2 - theoretical curve calculated using regression formulas
Analysis of the graphs indicates that the optimal soil density values are achieved with a drum amplitude of approximately $A \approx 0{,}1~\text{sm} $.
Figure 7 presents the results from a single-factor experiment examining how soil density varies with the oscillation frequency of the vibratory roller drum.
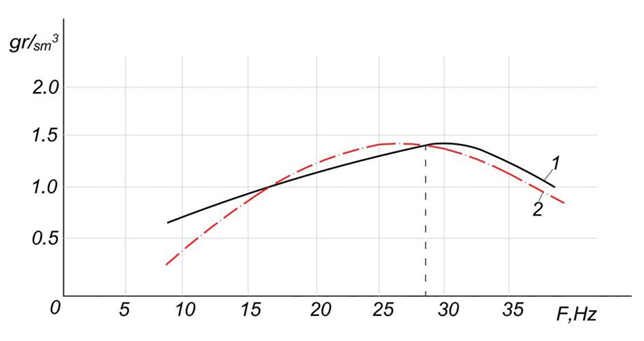
Fig. 7. Soil density versus vibratory roller drum frequency: 1 - experimental curve; 2 - theoretical curve calculated using regression formulas
The analysis of these graphs indicates that the optimal compaction frequency is approximately $F \approx 30~\text{Hz} $.
To assess the regularity of the influence of specific energy consumption on the physical model on the degree of soil compaction, a comparative diagram was drawn up, shown in Fig. 8.
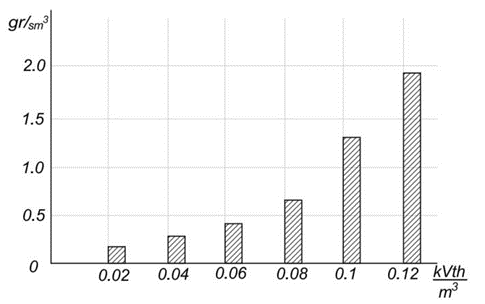
Fig. 8. Dependence of the degree of compaction of the roadbed on the specific energy consumption
Analysis of this diagram shows a significant nonlinearity in the dependence of the degree of compaction on specific energy consumption.
A preliminary examination reveals that the compaction process is influenced by numerous factors and exhibits significant nonlinearity. Therefore, it is essential to select a quadratic regression model and conduct a series of multivariate experiments, varying the factors based on the results obtained from single-factor experiments.
The implicit relationship between the factors and the optimization parameter can be expressed as follows:
| $Y = a_0 + \sum_i a_i x_i + \sum_{i,j} a_{ij} x_{ij} + \sum_i a_i x_i^2 $ | (12) |
where $Y$ is the value of the optimization parameter being considered; $x_i$ is the coded value of the factors (i=1, 2, 3, 4); $a_i$ is the value of the coefficient reflecting the contribution of the i-th factor; and $a_{ij}$ is the value of the coefficient describing the interaction between factors.
The experiments were conducted utilizing the Box-Behnken design, which accounts for complex interactions among factors. This design is known for its robustness and minimal susceptibility to variability in coefficient results. Additionally, varying the factors at three different levels ensures that the results are accurate, particularly at the lower points of the design. To validate the feasibility of the experiments, Cochran's test was employed to assess the hypothesis of equal variance for repeated measurements. The significance of the empirical coefficients in the regression equation was evaluated using Student's t-test with a significance level of 0.05. The adequacy of the adopted model to effectively represent the response surface was confirmed using standard methods.
| $F_{\text{рас}} < F_{\text{табл}}$ | (13) |
Table 1. Factors
|
№ |
Factor |
Code |
Factor Levels |
Range |
Dimensions |
||||
|
-1.68 |
-1 |
0 |
+1 |
+1.68 |
|||||
|
1 |
Vibratory drum compaction amplitude |
Х1 |
0.05 |
0.07 |
0.1 |
0.13 |
0.15 |
0.03 |
sm |
|
2 |
Compaction force |
Х2 |
1150 |
1300 |
1500 |
1700 |
1850 |
200 |
N |
|
3 |
Vibratory drum compaction frequency |
Х3 |
21.5 |
25 |
30 |
35
|
38.5 |
5 |
Hz |
|
4 |
Roller travel speed |
Х4 |
0,12 |
0,15 |
0,2 |
0,25 |
0,28 |
0,05 |
m/s |
3 Results and discussion
In several studies, machine design improvements were implemented on a modular basis according to technological requirements (Glavatsky et al.), without taking into account the complex factors that affect machine efficiency. Ter-Martirosyan's research primarily focused on the rheological properties of soil, but it did not examine their impact on machine design and technological parameters. Additionally, Mikheev's studies aimed at enhancing the design and technological aspects of a vibratory roller, yet they overlooked critical factors that influence the efficiency of the soil compaction process, such as soil moisture and inertial forces.
Experiments conducted using the Box-Behnken design method allowed for a systematic analysis of the key parameters affecting the effectiveness of subgrade compaction. By varying the compaction amplitude ($x_1$) from 0.05 to 0.15 sm, the compaction force ($x_2$) from 1150 to 1850 N, the vibratory drum compaction frequency ($x_3$) from 21.5 to 3.85 Hz, and the roller speed ($x_4$) from 0.12 to 0.28 m/s, a data matrix was created to provide a reliable estimate of the regression equation coefficients.
The mathematical model generated from the statistical data analysis demonstrated a strong correlation between the expected and actual compaction values. This selected model reached a 95% accuracy rate when compared to existing models. The excellent agreement between theory and practice confirms the adequacy of the selected factors and the validity of the experiments.
It was observed that as travel speed and compaction frequency increase, the rise in compaction coefficient tends to lag behind the rise in energy consumption. This suggests that a vibration roller designed with optimal parameters can not only enhance compaction productivity but also operate with minimal energy usage. Implementation of the research results, with some modifications, on a national scale in the Republic of Uzbekistan will significantly reduce the cost of roadbed construction and improve the efficiency of soil compaction.
After generating experimental data and verifying the significance of the regression coefficients, a mathematical model was developed to evaluate the performance of a prototype compaction machine.
| $Y=0,82+0,02X_1+0,08X_2-0,03X_3-0,02X_4+0,01X_1^2+0,02X_2^2-0,01X_(3 )^2-0,01X_4^2$ | (14) |
An assessment of the model's adequacy using the Fisher criterion showed that the mathematical model is adequate with a 95% confidence level.
| $F_{\text{рас}} = 0{,}95, \quad F_{\text{табл}} = 2{,}36 $ | (15) |
The model's adequacy requirement is met.
To determine the best factor values, equation (10) was tested for the maximum value; the results are presented in Table 2.
Table 2. Rational factor values
|
|
Factor |
|||
|
X1, sm |
X2, N |
X3, Hz |
X4, m/s |
|
|
Encoded |
0 |
+1 |
-1 |
-1 |
|
Natural |
0.1 |
1700 |
25 |
0.15 |
|
Rounded |
0.1 |
1700 |
25 |
0.15 |
Therefore, the optimal values for the key parameters of the compaction machine are:
- vibration roller compaction amplitude - A ≈ 0.1 sm;
- compaction force - P ≈ 1700 N;
- vibration roller compaction frequency - F ≈ 25 Hz;
- roller travel speed - ϑ ≈ 0.15 m/s.
4 Conclusions
The development and implementation of a physical model for the vibration roller enabled a thorough experimental analysis of the subgrade compaction process. In contrast to traditional trial-and-error methods commonly used in mechanical engineering, physical modeling significantly reduces material and time costs while allowing for rapid design modifications. This approach has proven effective in studying waste sorting technologies under controlled conditions.
Statistical evaluation of the experimental results indicated that the regression model is appropriate with a confidence level of 95%. The model accurately reflects the relationship between compaction efficiency and key influencing factors, including vibratory drum amplitude, compaction force, vibratory drum compaction frequency, and roller speed. This mathematical model serves as a reliable tool for predicting performance and optimizing machine settings across various operating conditions.
Based on experimental optimization, the following rational values were determined for the vibration roller:
- vibratory drum compaction amplitude - A ≈ 0.1 sm;
compaction force - P ≈ 1700 N;
- vibratory drum compaction frequency - F ≈ 25 Hz;
- roller speed - ϑ ≈ 0.15 m/s.
These parameters ensure maximum compaction efficiency while minimizing unnecessary energy and material costs.
The optimized vibration roller has the potential to significantly enhance roadbed compaction efficiency in Uzbekistan. The experimental findings pave the way for further research, particularly in integrating the proposed vibration roller, designed with optimal parameters, with other compaction technologies. Scaling the prototype to meet industrial demands will require studies on durability, maintenance needs, and long-term economic feasibility.
Acknowledgements
The authors declare no external funding was received.
References
- Zhang,Rui-Yuan.,Dai,Hong-Liang.,Wang,Yi-Die.(2022).Vibratory compaction response based on the contact model of roller-subgrade.Construction and Building Materials,Vol.351, Page 128798, DOI: https://doi.org/10.1016/j.conbuildmat.2022.128798
- Spagnoli,Giovanni.,Shimobe,Satoru.(2020).An over view on the compaction characteristics of soils by laboratory tests. Engineering Geology,Vol.278, Page 105830, DOI: https://doi.org/10.1016/j.enggeo.2020.105830
- Dan,Han-Cheng.,Yang Dong.,Liu, Xiang., Peng, An-Ping.,Zhang Zhi.(2020). Experimental investigation on dynamic response of asphalt pavement using SmartRock sensor under vibrating compaction loading. Construction and Building Materials,Vol.247, Page 118592, DOI: https://doi.org/10.1016/j.conbuildmat.2020.118592
- Pistrol, Johannes.,Hager Mario.,Kopf Frits and Adam,Dietmar.(2023).Consideration of the Variable Contact Geometry in Vibratory Roller Compaction.Infrastructures 2023,Vol.8(7),Page 110,DOI: https://doi.org/10.3390/infrastructures8070110
- Sharonov, Ivan., Kurdyumov Vladimir and Kurushin Viktor.(2019).The results of studies of eccentric tillage roller E3S Web of Conferences,Vol. 126, 00010 (2019). DOI: https://doi.org/10.1051/e3sconf/201912600010
- Nur Jihan Syamimi Jafri, Mohd Asri Ab Rahim, Mohd Zulham Affandi Mohd Zahid, Nor Faizah Bawadi, Muhammad Munsif Ahmad, Ahmad Faizal Mansor and Wan Mohd Sabki Wan Omar.(2018). Assessment of soil compaction properties based on surface wave techniques E3S Web of Conferences 34, 01002 (2018). DOI: https://doi.org/10.1051/e3sconf/20183401002
- Qinglong Zhang, Zaizhan An, Zehua Huangfu and Qingbin Li.(2022). A Review on Roller Compaction Quality Control and Assurance Methods for Earthwork in Five Application Scenarios. Materials 2022, 15(7), 2610. DOI: https://doi.org/10.3390/ma15072610
- Shanzhen Li, Yangsheng Ye, Liang Tang, Degou Cai, Shuang Tian and Xianzhang Ling.(2021). Experimental Study on the Compaction Characteristics and Evaluation Method of Coarse-Grained Materials for Subgrade. Materials 2021, Vol.14(1), 6972.DOI: https://doi.org/10.3390/ma14226972
- Glavatsky, Kazimir.,Cherkudinov, Volodymyr and Posmitiuha, Olexandr. (2018).Technical solutions for working elements of machines for efficient compaction of soil.MATEC Web of Conferences,Vol. 230,01006 (2018), DOI: https://doi.org/10.1051/matecconf/201823001006
- Ter–Martirsyan,Z.G., Ter–Martirsyan,A.Z., Sobolev, E.S.(2016).Vibration of Embedded Foundation at Multi–layered Base Taking into Account Non–linear and Rheological Properties of Soils. Procedia Engineering.Vol.153(7),747–753.DOI: https://doi.org/10.1016/j.proeng.2016.08.237
- Poulos, S.J. Compaction Control and the Index Unit Weight. / S.J. Poulos// Geotechnical Testing Journal.-1988.-Vol. 11(2), 100–108. DOI: https://doi.org/10.1520/GTJ10955J
- Kurdyumov,V.I.,Proshkin V.E.,Sharonov, I.A.,Proshkin E.N. and V.V.Dikov.(2023).Analysis of the influence on the structural composition of the soil of the main desing and rejime parameters of the vibratory roller.E3S Web of Conferences,Vol.392,020337.DOI: https://doi.org/10.1051/e3sconf/202339202037
- Capatina, Dragos.,Nitu,Marilena Cristina.,Iliescu,Mihaiela.(2023).Modeling the vibratory roller compaction process of road soil.Archives of civil engineering.Vol.LXIX,Issue4,431-444. DOI: https://doi.org/10.24425/ace.2023.147668
- Mikheev, V.V.,Saveliev,S.V.,Shushubaeva,M.K. Natural adaption of deformable work tools during vibratory soil compaction and enhancement of there performance.Journal of Physics:Conference Series.Vol.1260(6),1-6.DOI: https://doi.org/10.1088/1742-6596/1260/6/062015
- Khankelov, T., Askarkhodjayev, T., Aslanov N. Modeling of segmental excavator working tool for soil compaction. E3S Web of Conferences, 2023. DOI: https://doi.org/10.1051/e3sconf/202340102053
- Khankelov T.K., Norkuziev A.B. Segmented working element for a single-bucket excavator. Automation. Modern technologies. Vol. 79(8),345-347. DOI: https://doi.org/10.36652/0869-4931-2025-79-8-345-347
- T.K.Khankelov, A.Kh. Sarmonov, and A.G.Kadirov. The analytical dependence of the resistance force to digging with a bulldozer blade on the main influencing factors. E3S Web of Conferences 458, 10001 (2023), EMMFT-2023, DOI: https://doi.org/10.1051/e3sconf/202345810001
- T.K.Khankelov, A.G.Kadirov. Development of a method for physical modeling of the solid waste curing process using a dozer blade. AIP Conf. Proc. 3045.060035 (2024). DOI: https://doi.org/10.1063/5.0197343
- T.K.Khankelov, K.J.Rustamov, Komilov S.I.Application of rheological models in the study of compensation of road structure soils with cables. Acta of Turin Polytechnic University in Tashkent. Vol.1(4), 2023, 30, http://www.acta.polito.uz/
- Samandar Komilov. Distinctive features of vibrational compaction of subgrade soils with rollers. International multidisciplinary journal for research and development. Vol. 12(05), (2025), pp. 678-683, https://www.ijmrd.in/index.php/imjrd
- Balovnev, V.I. Optimization and Selection of Innovative Systems and Processes for Transport and Technological Machines. Study Guide. Moscow: Tekhpoligraftcentr, 2014. 392 p.
- Kramarenko, N.V. A Review of Methods for Deriving Similarity Criteria in Mechanics. Bulletin of Samara State Technical University. 2021, Vol.1(1), 163-192, https://www.mathnet.ru/vsgtu1791
- Khankelov, T.K., Rustamov, K.J., Irisbekova, M., Sabirova, D.K. Substantiation of the main parameters of a hammer crusher for grinding municipal solid waste.E3S Web of Conferences, 2024, 515, 03019, DOI: https://doi.org/10.1051/e3sconf/202451503019
- Khakimzyanov R., Ubaydullayev G. Formation of the complete technological bases of machine parts for mechanical processing. E3S Web of Conf. Vol. 531(1), 2024, DOI: https://doi.org/10.1051/e3sconf/202453101012
- Ubaydullayev, G. K., & Shadiev, S. R. (2024). Investigation of the deviation of the shape of the surfaces of parts on their performance. AIP Conference Proceedings, 3045(1), DOI: https://doi.org/10.1063/5.0197371
- Rashidbek Hudaykulov, Barno Salimova, Dilfuza Maxmudova, Dilshod Aralov. (2025). Effect of modifier on reinforced soil of subgrade.AIP Conf.Proc.3256, 0300002(2025), DOI: https://doi.org/10.1063/5.0266800
- Rashidbek Hudaykulov, Barno Salimova, Hurshid Abdullayev, Dilshod Aralov, Alimardon Esirgapov, (2025). Result of SEM analysis of strengthening of subgrade soil using modifier. AIP Conf.Proc.3256, 030014(2025), DOI: https://doi.org/10.1063/5.0266741
Conflict of Interest Statement
The authors declare no conflict of interest.
Author Contributions
Data Availability Statement
The study does not have a data set attached to it.
Supplementary Materials
There are no additional materials to include.