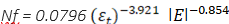Volume 23 article 1299 pages: 631-646
Received: Dec 17, 2024 Accepted: Oct 29, 2025 Available Online: Nov 19, 2025 Published: Dec 15, 2025
DOI: 10.5937/jaes0-55496
FLEXIBLE PAVEMENT REMAINING LIFE DUE TO ELASTIC MODULUS DECREASE BASED ON THE BINA MARGA 2017 METHOD AND THE ASPHALT INSTITUTE METHOD
Abstract
This research compares the remaining life of flexible pavement that experiences a decrease in elastic modulus due to road usage, utilizing The Bina Marga 2017 Method and The Asphalt Institute Method. The study begins with a structural evaluation of the pavement, field core sampling, and laboratory modulus testing. Variations in the asphalt mixture's elastic modulus are analyzed at 100%, 80%, and 60% of its original value for each layer. Using KENPAVE software, simulations determine the horizontal tensile strain on the bottom of asphalt layer to predict fatigue life and the vertical compressive strain on the top of subgrade for rutting life. The study also includes a traffic survey to assess traffic load, and remaining life calculations provide longevity predictions across both methods. The results indicate that a decrease in the elastic modulus value of the flexible pavement layer leads to a reduction in both fatigue life and rutting life, ultimately affecting the overall remaining life of the pavement. Notably, the remaining life assessments for fatigue and rutting calculated using The Bina Marga 2017 Method yield greater values than those determined by The Asphalt Institute Method. Therefore, it is recommended to utilize The Asphalt Institute Method for planning purposes, as it provides more conservative results, ensuring safer planning compared to The Bina Marga 2017 Method.
Highlights
- Decrease in elastic modulus value of the flexible pavement layer will shorten flexible pavement remaining life.
- The Asphalt Institute method provides more conservative and safer results than The Bina Marga 2017 Method.
- The KENPAVE simulation is used to analyze critical strain due to a decrease in elastic modulus, which is used to predict the remaining life of flexible pavement.
Keywords
Content
1 Introduction
Pavements often fail to reach their expected service life due to several influences. These factors can include unanticipated traffic growth, poor subgrade conditions, overloaded traffic loads, the use of inappropriate materials, environmental factors, and inconsistencies in implementation compared to the initial planning [1]-[7]. The remaining service life is primarily determined by damage from repeated loading, which increases over time. As the load repetitions accumulate, the condition of the pavement deteriorates, affecting its ability to accommodate traffic. This leads to issues such as fatigue and rutting [8]-[17]. Over time, these distresses compromise the structural integrity and surface quality of the pavement, resulting in decreased ride comfort, increased maintenance needs, and higher lifecycle costs. If not addressed promptly, the progression of damage can lead to more severe failures, ultimately shortening the pavement's service life [18-27]. Fatigue and rutting significantly influence the remaining life of flexible pavements [28]-[32]. Common performance assessment indicators for flexible pavements include fatigue cracking beneath the asphalt layer and rutting at the surface level, both of which are important for evaluating the structural performance of the pavement. However, calculating the stress and strain responses in each layer of the pavement structure manually can be quite challenging due to the need for high accuracy.
The elastic modulus of flexible pavement layers decreases with road usage and environmental factors, such as weather. This reduction in the elastic modulus directly impacts the fatigue life, rutting life, and overall remaining lifespan of the flexible pavement. Therefore, it is essential to conduct research on a pavement section to assess the fatigue life, rutting life, and remaining life of flexible pavement that has experienced a decrease in the elastic modulus of its layers.
An innovative approach is necessary to address the challenges associated with flexible pavements, particularly in predicting their fatigue life, rutting life, and remaining life when there is a decrease in the elastic modulus of the pavement layers. This analysis will employ two methods: The Bina Marga 2017 Method [33] and The Asphalt Institute Method. The aim is to find effective solutions for managing damage to flexible pavements. Additionally, the research will compare the results obtained from these two methods to determine which one is more suitable for application to flexible pavements in Indonesia. This study intends to evaluate the remaining life of flexible pavements as their elastic modulus decreases over time with usage. Ultimately, the research contributes to the advancement of knowledge, particularly for professionals involved in road construction, design engineers, and relevant agencies working with flexible pavements.
2 Materials and methods
The research approach consists of several methods. It begins with field observations, which include assessing the thickness and type of material in each pavement layer. After this, test samples are collected using a core drill and transported to the laboratory for Indirect Tensile Stiffness Modulus (ITSM) testing. The evaluation of the flexible pavement structure, along with the ITSM test results, will be used as input for the KENPAVE software. This will generate outputs in the form of horizontal tensile strain on the bottom of asphalt layer and vertical compressive strain on the top of subgrade. The output of the KENPAVE software will be utilized to calculate the fatigue life and rutting life of flexible pavement. By analyzing these calculations alongside traffic load data obtained from traffic surveys, we will predict the remaining life of the pavement. The remaining life of the flexible pavement will be determined using two different methods: The Asphalt Institute Method and The Bina Marga 2017 Method. The goal of this research is to provide a recommendation for the most suitable method for application in Indonesia, based on the assessed fatigue life, rutting life, and remaining life of flexible pavement that has experienced a decrease in elastic modulus within its layers. An overview of the research methodology is illustrated in Figure 1.
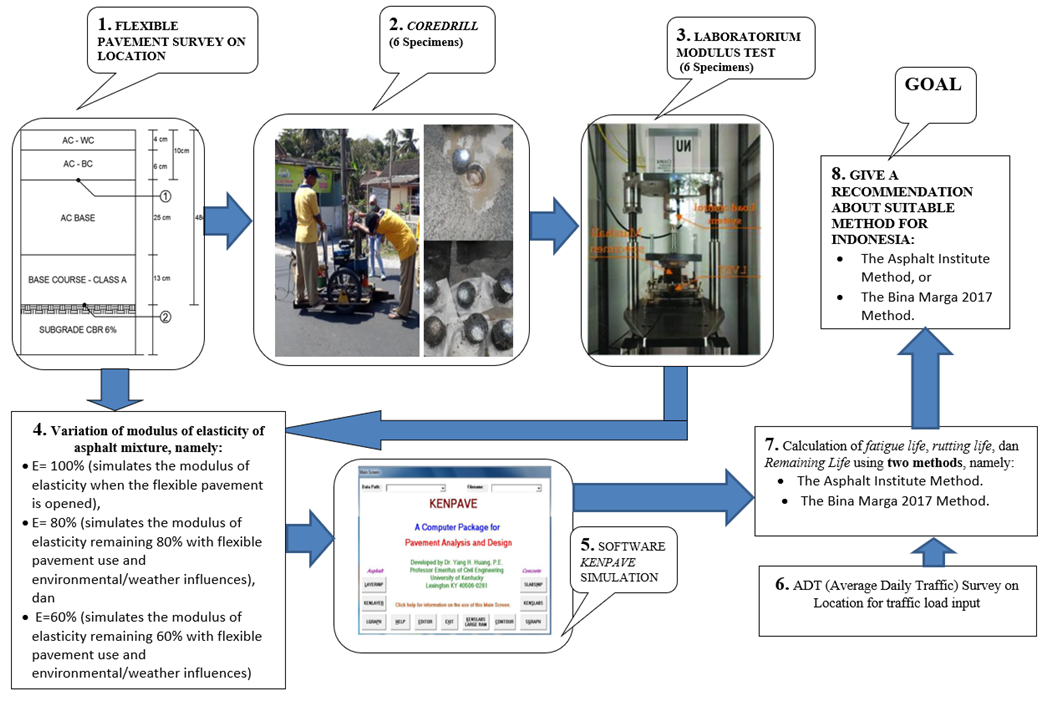
Fig. 1. Research method illustration
The research consisted of eight stages, namely:
2.1 Stage 1
Stage 1: Literature study on fatigue life, rutting life, and remaining life of flexible pavement. Additionally, it evaluates the structure of flexible pavement, including the thickness and material type of each layer. The research was conducted on Ir. Juanda Road in Surakarta, Indonesia as illustrated in Figure 2. The evaluation results for the flexible pavement section can be found in Figure 3.
Fig. 2. Research Location on Ir.Juanda Road Surakarta City, Indonesia (Source: Google Earth, 2023)
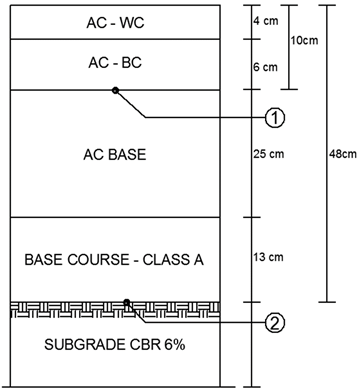
Fig. 3. Existing Flexible Pavement Structure
2.2 Stage 2
Stage 2: Sampling of test specimens will be conducted in the field using a core drill. The core drill, operated with a specialized machine tool as shown in Figure 4, will produce cylindrical test samples measuring 4 inches in diameter and 6.3 centimeters in height. In this study, six core drill samples will be collected from six different locations on the flexible pavement section.

Fig. 4. (a) Coredrill Machine (b) Coredrill sample illustration
2.3 Stage 3
Stage 3: Conduct ITSM (Indirect Tensile Stiffness Modulus) testing on coredrill specimens. Additionally, six coredrill specimens will be tested for ITSM, as shown in Figure 5.

Fig. 5. Indirect tensile stiffness modulus (ITSM) test
2.4 Stage 4
Stage 4: According to the modulus test results from the laboratory and the evaluation of flexible pavement in the field, variations in the elastic modulus of the asphalt mixture will be tested, specifically at 100%, 80%, and 60%. E = 100% (simulates the elastic modulus when the road is newly opened); E = 80% (simulates the elastic modulus remaining at 80% due to road usage and the effects of environmental conditions); E = 60% (simulates the elastic modulus remaining at 60%, also accounting for road usage and environmental influences). These variations will be applied to each layer of flexible pavement.
2.5 Stage 5
Stage 5: Based on the data regarding the variation of elastic modulus values in the pavement layer, we will conduct a design simulation of the flexible pavement thickness using KENPAVE software. This simulation aims to determine the horizontal tensile strain occurring on the bottom of the asphalt layer to predict the fatigue life of the flexible pavement, as well as the vertical compressive strain on the top of subgrade to estimate the rutting life. The main interface of the KENPAVE program is illustrated in Figure 6.
Fig. 6. KENPAVE Program Main View [34]
2.6 Stage 6
Stage 6: Calculation of fatigue life and rutting life. Calculation of fatigue life and rutting life using two methods, namely The Asphalt Institute Method and The Bina Marga 2017 Method [33].
2.7 Stage 7
Stage 7: Average Daily Traffic (ADT) survey on the road section to calculate the traffic load. The ADT survey was conducted for three days, namely Monday, Thursday and Sunday to determine the volume of traffic passing through the flexible pavement section. The traffic survey was conducted by 6 personnel per day, 3 personnel counted the traffic volume in one lane direction and 3 other personnel counted the traffic volume in the other lane direction. An overview of the LHR Survey is illustrated in Figure 7.
Fig. 7. Illustration of Average Daily Traffic (ADT) Survey
2.8 Stage 8
Stage 8: The calculation of the remaining life of flexible pavement is based on two primary factors: fatigue life and rutting life. These factors help predict the pavement's longevity during its planned service life. There are two methods for calculating the remaining life of flexible pavement: The Asphalt Institute Method and The Bina Marga 2017 Method. Then compare the two methods and recommend the most suitable one for flexible pavement in Indonesia.
3 Results and Discussion
This research has potential limitations. Despite the thorough approach adopted in this study, several limitations must be acknowledged: Variations in Material Properties (The material properties used in the analysis were based on assumed or average values from literature or standard specifications. In practice, materials such as asphalt, base, and subgrade layers can exhibit significant variability due to differences in local sourcing, construction practices, and aging. This variability may affect the actual pavement performance compared to the simulation results), Environmental Factors (The impact of environmental conditions—such as temperature fluctuations, freeze-thaw cycles, and moisture variations—was not fully incorporated into the simulations. These factors can substantially influence material behavior and pavement lifespan, introducing uncertainties when extrapolating the results to real-world conditions), Uncertainties in KENPAVE Simulations (While KENPAVE is a widely recognized tool for pavement analysis, it operates under certain simplifying assumptions (e.g., linear elastic behavior of materials, static loading). These assumptions may not capture the complex, nonlinear, and time-dependent nature of pavement response under actual traffic and environmental loading. Consequently, the predictions may deviate from actual field performance), Limited Scope of Load and Traffic Considerations (The research considered a specific range of traffic loading scenarios. However, variations in axle loads, loading repetitions, and traffic growth over time were not comprehensively modeled, which could affect the long-term accuracy of the simulation outcomes), and Model Calibration and Validation (The simulations were not calibrated or validated against extensive field data, which is essential for improving the reliability of the predictive models. As a result, the findings should be interpreted with caution until further validation is conducted).
3.1 Test Results of Modulus of Elasticity of Flexible Pavement Layer
The results of the elastic modulus testing for the flexible pavement layers and the simulation of the elastic modulus of the degraded material are summarized in Table 1. The elastic modulus values are as follows: E= 100% represents the modulus when the road is first opened; E= 80% simulates the modulus after road use and environmental influences reduces it to 80%; and E= 60% reflects the modulus after further degradation to 60% due to continued pavement use and environmental factors on each layer of flexible pavement.
Table 1. Test Results of Elastic Modulus of Flexible Pavement Layers
|
|
Elastic Modulus of flexible pavement layers, E (kPa) |
||
|
Flexible Pavement Layers |
E=100 % (Testing results) |
E=80 % |
E=60 % |
|
Asphalt Concrete-Wearing Course (AC-WC) |
1,100,000 |
880,000 |
660,000 |
|
Asphalt Concrete-Binder Course (AC-BC) |
1,200,000 |
960,000 |
720,000 |
|
Asphalt Concrete-Base (AC-BASE) |
1,600,000 |
1,280,000 |
960,000 |
|
Base Course |
300,000 |
240,000 |
180,000 |
|
Subgrade |
60,000 |
48,000 |
36,000 |
3.2 Flexible Pavement Structure of Ir.Juanda Road Surakarta City
Simulation of flexible pavement structures will be conducted to examine the effect of decreasing the elastic modulus on the remaining service life of the flexible pavement, as shown in Figure 8.
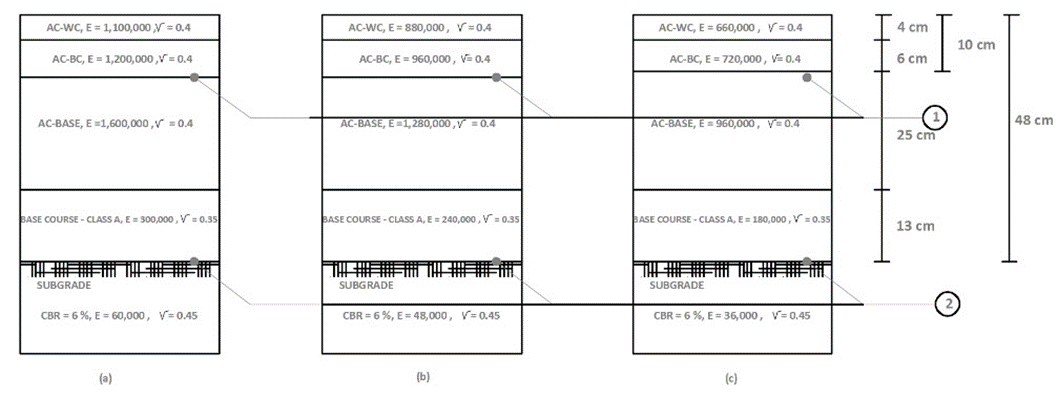
Fig. 8. Flexible Pavement Structure of Ir.Juanda Road Surakarta City (a) The elastic modulus for the newly opened road is 100%; (b) Elastic modulus remaining 80% (c) Elastic modulus remaining 60%
3.3 ADT Survey Results and Calculation of Equivalent Standard Axle Load (ESA) and Cumulative Equivalent Standard Axle Load (CESA) of Flexural Pavement during the Design Life
The results of the Average Daily Traffic (ADT) survey and ESA Value Calculation can be seen in Table 2. The calculation of CESA 4 value for 20 years is presented in Table 3, and the calculation of CESA 5 value for 20 years is presented in Table 4.
Table 2. ADT Survey Results and ESA Calculation
|
Type of Vehicle |
Description |
2022 ADT (vehicle) |
VDF 4 |
VDF 5 |
DD |
DL |
ESA4 (ESAL) |
ESA5 (ESAL) |
|
1 |
Motorcycles |
7,752 |
0 |
0 |
0.5 |
1 |
0 |
0 |
|
2 |
Sedan, Jeep, & Station Wagon |
2,894 |
0 |
0 |
0.5 |
1 |
0 |
0 |
|
3 |
Pick Up, Combi, & Minibus |
4,854 |
0 |
0 |
0.5 |
1 |
0 |
0 |
|
4 |
Pick Up & Mini Truk |
2,726 |
0 |
0 |
0.5 |
1 |
0 |
0 |
|
5A |
Light bus |
1,101 |
0.3 |
0.2 |
0.5 |
1 |
165,15 |
110 |
|
5B |
Heavy bus |
179 |
1 |
1 |
0.5 |
1 |
89,5 |
89,5 |
|
6A |
2 Axle light truck |
120 |
0.55 |
0.5 |
0.5 |
1 |
33 |
30 |
|
6B |
2 Axle heavy truck |
65 |
4 |
5.1 |
0.5 |
1 |
130 |
165,75 |
|
7A1 |
3 Axle light truck |
50 |
4.7 |
6.4 |
0.5 |
1 |
117,5 |
160 |
|
7A2 |
3 Axle heavy truck |
5 |
4.7 |
6.4 |
0.5 |
1 |
11,75 |
16 |
|
8 |
Un Motor |
259 |
0 |
0 |
0.5 |
1 |
0 |
0 |
|
Total CESA |
437,4 |
457 |
||||||
Table 3. Calculation result of CESA 4 for 20 years
|
Year to |
ESA |
R |
CESA 4 (ESAL) |
|
1 |
437,4 |
1.00 |
159,651 |
|
2 |
|
2.048 |
326,965 |
|
3 |
|
3.146 |
502,62 |
|
4 |
|
4.297 |
686,020 |
|
5 |
|
5.503 |
878,559 |
|
6 |
|
6.767 |
1,080,358 |
|
7 |
|
8.092 |
1,291,895 |
|
8 |
|
9.841 |
1,571,125 |
|
9 |
|
10.936 |
1,745,943 |
|
10 |
|
12.461 |
1,989,411 |
|
11 |
|
14.059 |
2,244,533 |
|
12 |
|
15.734 |
2,511,948 |
|
13 |
|
17.489 |
2,792,136 |
|
14 |
|
19.328 |
3,085,734 |
|
15 |
|
21.256 |
3,393,541 |
|
16 |
|
23.276 |
3,716,036 |
|
17 |
|
25.394 |
4,054,177 |
|
18 |
|
27.613 |
4,408,443 |
|
19 |
|
29.938 |
4,779,631 |
|
20 |
|
32.275 |
5,152,736 |
Table 4. Calculation result of CESA 5 for 20 years
|
Year to |
ESA |
R |
CESA 5 (ESAL) |
|
457 |
1.00 |
166,805 |
|
|
2 |
|
2.048 |
341,616 |
|
3 |
|
3.146 |
524,768 |
|
4 |
|
4.297 |
716,761 |
|
5 |
|
5.503 |
917,927 |
|
6 |
|
6.767 |
1,128,769 |
|
7 |
|
8.092 |
1,349,786 |
|
8 |
|
9.841 |
1,641,528 |
|
9 |
|
10.936 |
1,824,179 |
|
10 |
|
12.461 |
2,078,557 |
|
11 |
|
14.059 |
2,345,111 |
|
12 |
|
15.734 |
2,624,509 |
|
13 |
|
17.489 |
2,917,252 |
|
14 |
|
19.328 |
3,224,007 |
|
15 |
|
21.256 |
3,545,607 |
|
16 |
|
23.276 |
3,882,553 |
|
17 |
|
25.394 |
4,235,846 |
|
18 |
|
27.613 |
4,530,924 |
|
19 |
|
29.938 |
4,993,808 |
|
20 |
|
32.275 |
5,383,631 |
3.4 Flexible pavement response affected by reduced elastic modulus
The flexible pavement response refers to the strain occurring on the bottom of asphalt layer, which is determined using the elastic modulus values for different variations (100%, 80%, and 60%). This data is essential for predicting the pavement's fatigue life. Additionally, the vertical compressive strain on the top of subgrade, which is also based on these elastic modulus variations, helps in predicting rutting life. The results are summarized in Table 5 and illustrated in Figure 9. The flexible pavement response is obtained using KENPAVE software.
Table 5. Strain occurring in flexible pavement for each variation of elastic modulus (i.e. 100%, 80%, and 60%)
|
Depth (cm) |
E= 100 % |
E= 80 % |
E= 60 % |
|||
|
ɛh |
ɛv |
ɛh |
ɛv |
ɛh |
ɛv |
|
|
10 |
0.003326 |
- |
0.004157 |
- |
0.005543 |
- |
|
48 |
- |
0.001123 |
- |
0.001164 |
- |
0.001551 |
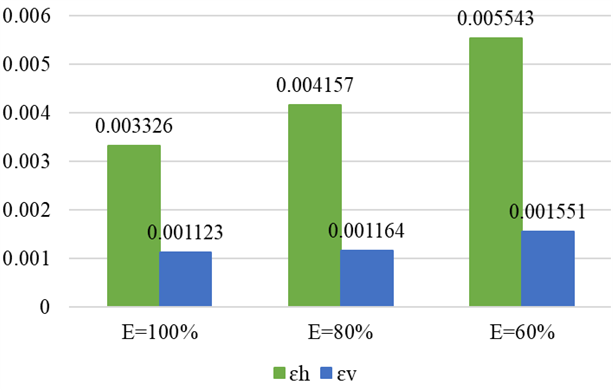
Fig. 9. Strain occurring in flexible pavement for each variation of elastic modulus (i.e. 100%, 80%, and 60%)
According to Table 5 and Figure 9, the horizontal tensile strain occurring on the bottom of asphalt layer increases as the elastic modulus decreases, particularly at a depth of 10 cm. This trend is also observed in the vertical compressive strain on the top of subgrade, which is measured at a depth of 48 cm. As the elastic modulus value decreases, both the horizontal tensile strain on the bottom of asphalt layer and the vertical compressive strain on the top of subgrade become more pronounced. This is because a lower elastic modulus indicates a reduction in the strength quality of the flexible pavement layer. As a result, the flexible pavement becomes less capable of supporting traffic loads and is more susceptible to weather effects, resulting in increased horizontal tensile strain on the bottom of asphalt layer and greater vertical compressive strain on the top of subgrade.
3.5 Fatigue life of flexible pavement affected by decrease in elastic modulus
In this research, the fatigue life of flexible pavement will be predicted using two equations proposed by The Asphalt Institute and The Bina Marga 2017.
Fatigue life will be calculated using the elastic modulus values for different variations: 100%, 80%, and 60%. This will be based on the horizontal tensile strain occurring at a depth of 10 cm beneath the asphalt layer. Two methods will be employed for this calculation: The Asphalt Institute Method and The Bina Marga Method. To determine fatigue life using the Bina Marga 2017 Method, we will use Equation 1. For calculations using The Asphalt Institute Method, we will refer to Equation 2.
|
|
(1) |
|
|
(2) |
The results of the calculation for the fatigue life of flexible pavement, which is influenced by reductions in the modulus of elasticity (specifically at levels of 100%, 80%, and 60%), are presented in Table 6 and Figure 10. This analysis is based on both The Bina Marga 2017 Method and The Asphalt Institute Method.
Table 6. The results of the calculation of the fatigue life of flexible pavement affected by decrease of elastic modulus (namely 100%, 80%, and 60%) based on The Bina Marga 2017 Method and The Asphalt Institute Method
|
Method |
Fatigue Life, Nf (ESAL) |
||
|
E=100% |
E=80% |
E=60% |
|
|
The Bina Marga 2017 Method |
16,324,224 |
14,817,512 |
11,124,596 |
|
The Asphalt Institute Method |
|||
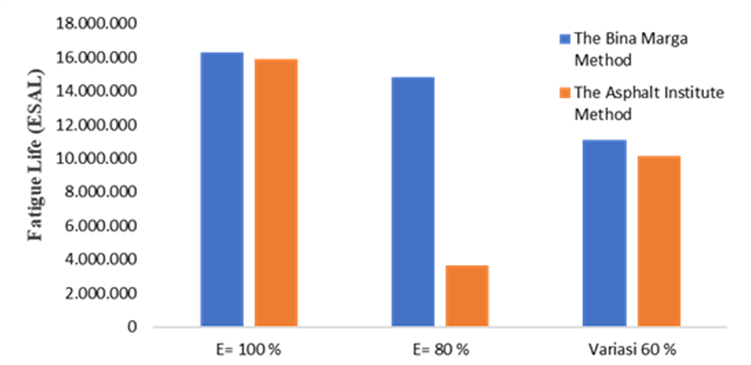
Fig. 10. Relationship Graph of Fatigue Life utilizing The Bina Marga 2017 Method and The Asphalt Institute Method with Variations in the Decrease of Elastic Modulus
Based on Table 6 and Figure 10, it can be seen that the fatigue life of flexible pavement will decrease along with the decrease in the elastic modulus of the flexible pavement layer. This occurs in the calculation of fatigue life with The Bina Marga 2017 Method and The Asphalt Institute Method. Fatigue life of the flexible pavement is predicted using the horizontal tensile strain on the bottom of asphalt layer at a depth of 10 cm.
The fatigue life calculated using The Bina Marga 2017 Method is greater than that calculated using The Asphalt Institute method. According to The Asphalt Institute method, the initial fatigue life value at the beginning of road use is 15,924,224 Equivalent Single Axle Loads (ESAL). After a decrease in elastic modulus, the fatigue life drops to 13,652,211 ESAL with 80% remaining elastic modulus and further declines to 10,164,556 ESAL with 60% remaining elastic modulus. In contrast, The Bina Marga 2017 Method gives an initial fatigue life of 16,324,224 ESAL. After experiencing a decrease in elastic modulus, this value reduces to 14,817,512 ESAL with 80% remaining elastic modulus and to 11,124,596 ESAL with 60% remaining elastic modulus, underscores the need for careful consideration of pavement materials and conditions during maintenance planning [35].
Additionally, the impact on fatigue life becomes more pronounced as elastic modulus decreases, which results in lower ESAL values. This emphasizes structural integrity considerations in pavement design and maintenance planning. It is imperative for Engineers and Decision-Makers to critically assess which method provides the most reliable predictions for their specific conditions [36].
The evaluation of fatigue life values is critical for effective decision-making in pavement maintenance, particularly when comparing methodologies such as The Bina Marga 2017 Method and The Asphalt Institute Method. Observations indicate that the fatigue life diminishes as the elastic modulus of flexible pavement decreases. This trend is supported by findings that highlight the significant contributions of high temperatures and heavy axle loads to rutting development in asphalt pavements, which ultimately affect overall performance and durability [37].
3.6 Rutting life of flexible pavement affected by decrease in elastic modulus
Rutting life will be assessed based on the elastic modulus for three variations: 100%, 80%, and 60%. This will be analyzed in relation to the vertical compressive strain on the top of subgrade at a depth of 48 cm. Two methods will be employed for this calculation: The Bina Marga 2017 Method and The Asphalt Institute Method. The Rutting Life will be calculated using Equation 3 for The Bina Marga 2017 Method and Equation 4 for The Asphalt Institute Method. Detailed calculations of rutting life can be found in Table 7 and illustrated in Figure 11.
|
Nr = (9300/εc )⁷ |
|
(3) |
|
Nr = 1.365 × 10⁻⁹ · (εc )⁻⁴.⁴⁷ |
|
(4) |
where:
- Nr = Number of load repetitions to achieve rutting/Rutting life (ESAL)
- εc = Vertical compressive strain on the top of subgrade
Table 7. Results of the calculation of the rutting life of flexible pavement affected by decrease of elastic modulus (namely 100%, 80%, and 60%) based on The Bina Marga 2017 Method and The Asphalt Institute Method
|
Method |
Rutting Life, Nr (ESAL) |
||
|
E=100 % |
E=80 % |
E=60 % |
|
|
The Asphalt Institute Method |
4,452,213 |
||
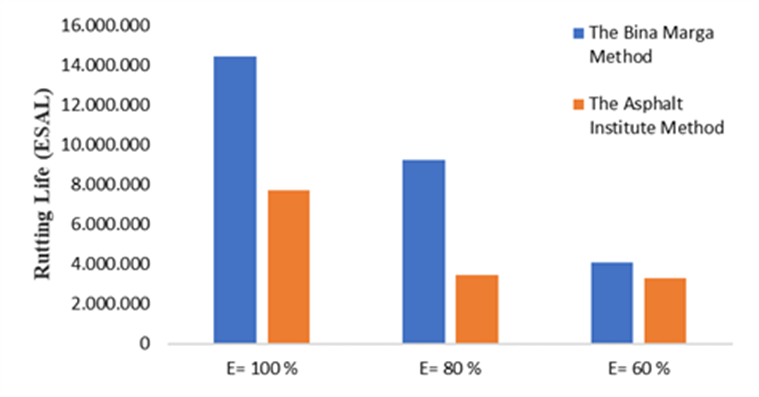
Fig. 11. Relationship Graph of Rutting Life utilizing The Bina Marga 2017 Method and The Asphalt Institute Method with Variations in the Decrease of Elastic Modulus
The rutting life calculated using The Bina Marga 2017 Method yields a higher initial value than The Asphalt Institute Method, suggesting potential advantages in predictive reliability. Specifically, The Bina Marga 2017 Method indicates an initial life of 13,347,177 Equivalent Single Axle Loads (ESAL) compared to 6,739,505 ESAL according to the Asphalt Institute method. Notably, the decrement in rutting life upon reduction of elastic modulus (with values dropping to 9,251,909 ESAL and 4,452,213 ESAL at 80% modulus, respectively)
Cheng et al. affirm the importance of accurate performance predictions for effective pavement management, particularly highlighting how rutting and fatigue metrics influence maintenance decisions [38]. Moreover, the differential outcomes of the methodologies underline the need to select appropriate design and evaluation methods based on specific environmental and traffic conditions.
For instance, the consistent predictions of The Bina Marga 2017 Method across various elastic modulus levels could lead to more robust maintenance strategies; this is supported by research that compares various pavement condition assessment methods, affirming the effectiveness of The Bina Marga 2017 Method in practical evaluations [39].
Understanding the implications of altered elastic modulus not only aids in immediate maintenance scheduling but also aligns long-term strategy with structural resilience goals. In summary, the comparative analysis of rutting life data reveals significant insights into how variations in elastic modulus influence pavement performance and maintenance strategies. This critical understanding will enable more informed decision-making, aligning design methodologies with expected service conditions and ultimately prolonging pavement life.
3.7 Remaining Life Due to Fatigue and Rutting Affected by Decrease in Elastic Modulus
The remaining life due to fatigue and rutting will be determined using Equation 5.
| (5) |
where:
- RL = Remaining Life (%)
- Np = Total Traffic to date (ESAL)
- N1.5 = Total Traffic to pavement failure (ESAL)
- N1.5 Fatigue = Nf (Table 6)
- N1.5 Rutting = Nr (Table 7)
Table 8 and Figure 12 present the calculation of the remaining life due to fatigue and rutting affected by the decrease in elastic modulus of the flexible pavement layer using The Bina Marga 2017 Method, while those using The Asphalt Institute Method are presented in Table 9 and Figure 13.
Table 8. Calculation of remaining life due to fatigue and rutting affected by decrease in elastic modulus of the flexible pavement layer using The Bina Marga 2017 Method
|
Year to |
Np=CESA5 (ESAL) |
Remaining life due to fatigue (%) |
Remaining life due to rutting (%) |
||||
|
E= 100% |
E= 80% |
E= 60% |
E= 100% |
E= 80% |
E= 60% |
||
|
1 |
166,805 |
98.98 |
98.8 |
98.3 |
98.8 |
98.2 |
96.3 |
|
2 |
341,616 |
97.9 |
97.6 |
96.6 |
97.6 |
96.3 |
92.4 |
|
3 |
524,768 |
96.7 |
96.4 |
94.8 |
96.3 |
94.3 |
88.3 |
|
4 |
716,761 |
95.6 |
95.1 |
92.9 |
95.0 |
92.2 |
84.1 |
|
5 |
917,927 |
94.3 |
93.7 |
90.9 |
93.6 |
90.1 |
79.5 |
|
6 |
1,128,769 |
93.1 |
92.3 |
88.8 |
92.2 |
87.8 |
74.8 |
|
7 |
1,349,786 |
91.7 |
90.8 |
86.7 |
90.6 |
85.4 |
69.9 |
|
8 |
1,641,528 |
89.9 |
88.8 |
83.8 |
88.6 |
82.2 |
63.5 |
|
9 |
1,824,179 |
88.8 |
87.6 |
82.1 |
87.4 |
80.2 |
59.4 |
|
10 |
2,078,557 |
87.3 |
85.8 |
79.5 |
85.6 |
77.5 |
53.7 |
|
11 |
2,345,111 |
85.6 |
84.1 |
76.9 |
83.7 |
74.6 |
47.8 |
|
12 |
2,624,509 |
83.9 |
82.2 |
74.2 |
81.8 |
71.6 |
41.6 |
|
13 |
2,917,252 |
82.1 |
80.1 |
71.2 |
79.8 |
68.5 |
35.1 |
|
14 |
3,224,007 |
80.2 |
78.1 |
68.3 |
77.6 |
65.2 |
28.3 |
|
15 |
3,545,607 |
78.3 |
75.9 |
65.1 |
75.4 |
61.6 |
21.1 |
|
16 |
3,882,553 |
76.2 |
73.6 |
61.8 |
73.1 |
58.0 |
13.6 |
|
17 |
4,235,846 |
74.1 |
71.2 |
58.3 |
70.6 |
54.2 |
5.8 |
|
18 |
4,530,924 |
72.2 |
69.2 |
55.4 |
68.6 |
51.0 |
failure |
|
19 |
4,993,808 |
69.4 |
66.1 |
50.8 |
65.4 |
46.0 |
|
|
20 |
5,383,631 |
67.0 |
63.4 |
47.0 |
62.7 |
41.8 |
|
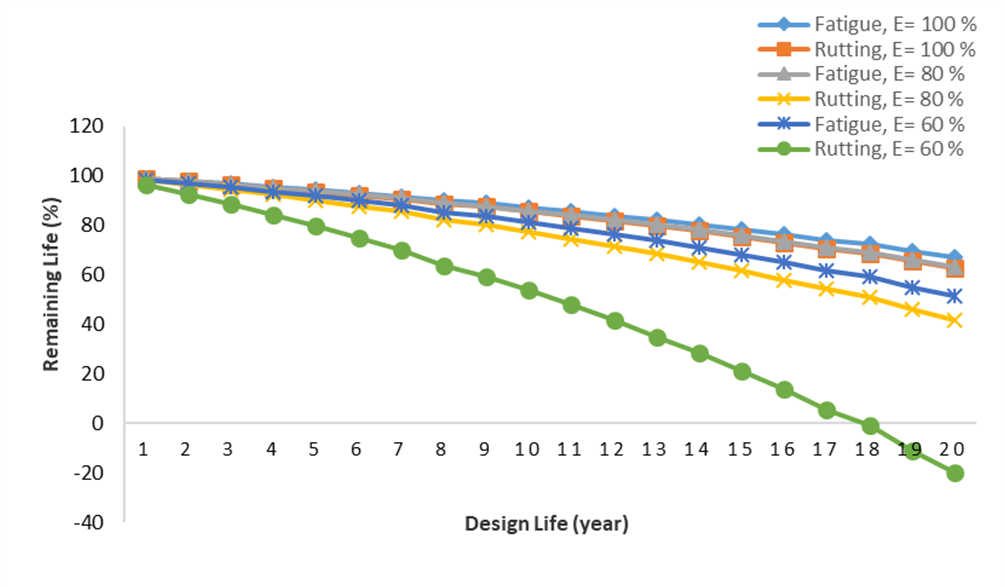
Fig. 12. Remaining life due to fatigue and rutting influenced by decrease in elastic modulus of flexible pavement layers using The Bina Marga 2017 Method
Table 9. Calculation of remaining life due to fatigue and rutting affected by decrease in elastic modulus of the flexible pavement layer using The Asphalt Institute Method
|
Year to |
Np= CESA5 (ESAL) |
Remaining life due to fatigue (%) |
Remaining life due to rutting (%) |
||||
|
E= 100% |
E= 80% |
E= 60% |
E= 100% |
E= 80% |
E= 60% |
||
|
1 |
166,805 |
98.9 |
95.7 |
91.3 |
98.8 |
95.4 |
94.9 |
|
2 |
341,616 |
97.8 |
91.3 |
86.7 |
97.6 |
90.6 |
89.6 |
|
3 |
524,768 |
96.7 |
86.2 |
81.8 |
96.3 |
85.6 |
84.1 |
|
4 |
716,761 |
95.4 |
81.8 |
76.7 |
95.0 |
80.3 |
78.3 |
|
5 |
917,927 |
94.2 |
76.7 |
71.4 |
93.6 |
74.8 |
72.2 |
|
6 |
1,128,769 |
92.9 |
71.4 |
65.8 |
92.2 |
69.1 |
65.8 |
|
7 |
1,349,786 |
91.5 |
65.8 |
58.4 |
90.6 |
63.0 |
59.1 |
|
8 |
1,641,528 |
89.6 |
58.4 |
53.8 |
88.6 |
55.1 |
50.3 |
|
9 |
1,824,179 |
88.5 |
53.8 |
47.4 |
87.3 |
50.1 |
44.7 |
|
10 |
2,078,557 |
86.9 |
47.4 |
40.6 |
85.6 |
43.1 |
37.1 |
|
11 |
2,345,111 |
85.2 |
40.6 |
33.5 |
83.7 |
35.7 |
29.0 |
|
12 |
2,624,509 |
83.5 |
33.5 |
26.1 |
81.8 |
28.1 |
20.5 |
|
13 |
2,917,252 |
81.6 |
26.2 |
18.4 |
79.8 |
20.1 |
11.7 |
|
14 |
3,224,007 |
79.7 |
18.4 |
10.2 |
77.6 |
11.7 |
2.4 |
|
15 |
3,545,607 |
77.7 |
10.3 |
1.7 |
75.4 |
2.9 |
failure |
|
16 |
3,882,553 |
75.6 |
1.7 |
failure |
73.1 |
failure |
|
|
17 |
4,235,846 |
73.3 |
failure |
|
70.6 |
|
|
|
18 |
4,530,924 |
71.5 |
|
|
68.6 |
|
|
|
19 |
4,993,808 |
68.6 |
|
|
65.4 |
|
|
|
20 |
5,383,631 |
66.2 |
|
|
62.7 |
|
|
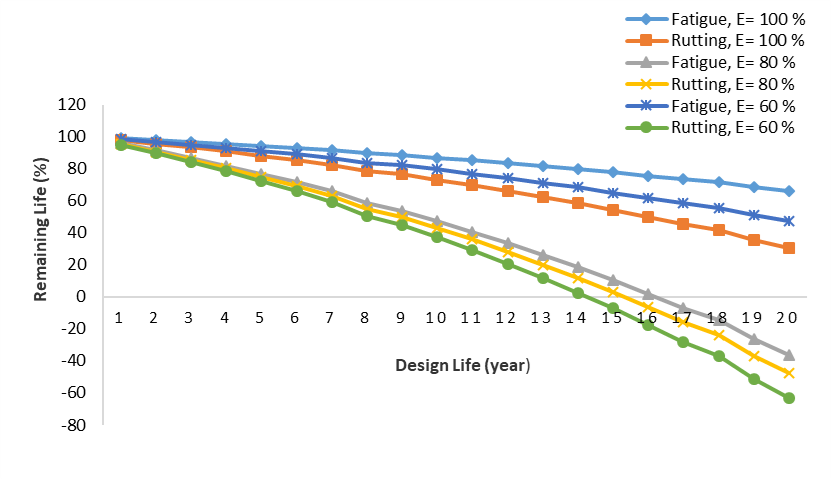
Fig. 13. Remaining life due to fatigue and rutting influenced by decrease in elastic modulus of flexible pavement layers using The Asphalt Institute Method
Figure 12 shows that remaining life due to fatigue and rutting calculated using The Bina Marga 2017 Method tends to decrease as the elastic modulus of the flexible pavement layer decreases. Remaining life to fatigue and rutting calculated using The Asphalt Institute Method also decreases as the elastic modulus of the flexible pavement layer decreases, as can be seen in Figure 13.
3.7 Comparison of Remaining Life due to Fatigue and Rutting Using The Bina Marga 2017 Method and The Asphalt Institute Method
Comparison of remaining life due to fatigue and rutting using The Bina Marga 2017 Method and The Asphalt Institute Method at each value of elastic modulus of flexible pavement layer is presented in Figure 14 to Figure 16.
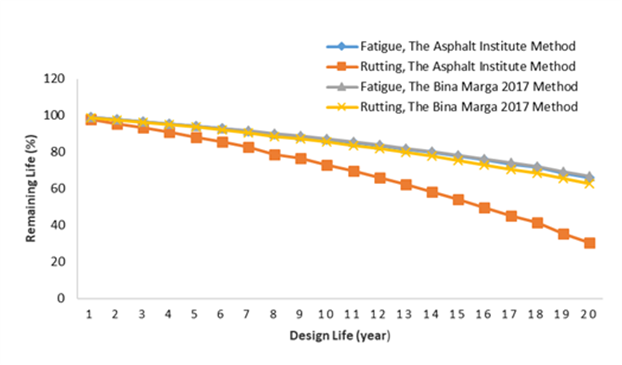
Fig. 14. Comparison of Remaining Life due to Fatigue and Rutting Using The Bina Marga 2017 Method and The Asphalt Institute Method at 100% elastic modulus
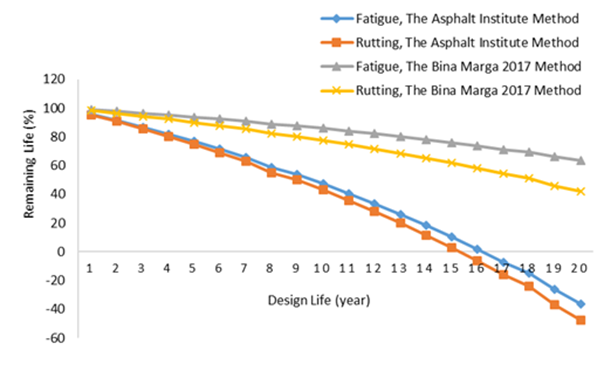
Fig. 15. Comparison of Remaining Life due to Fatigue and Rutting Using The Bina Marga 2017 Method and The Asphalt Institute Method at 80% elastic modulus
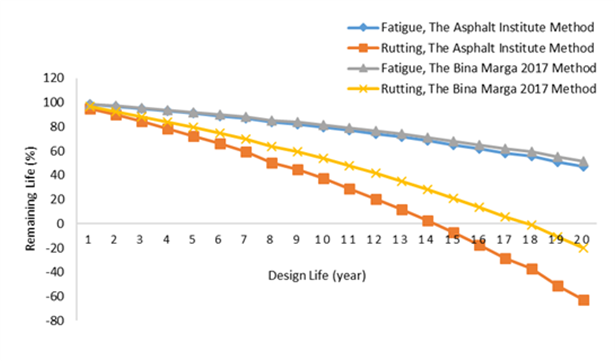
Fig. 16. Comparison of Remaining Life due to Fatigue and Rutting Using The Bina Marga 2017 Method and The Asphalt Institute Method at 60% elastic modulus
Based on Figures 14-16, the remaining life due to fatigue and rutting at all elastic modulus values is greater when using The Bina Marga 2017 Method compared to The Asphalt Institute Method. Additionally, the remaining life due to fatigue is longer than that for rutting, indicating that rutting damage is more critical than fatigue damage. Improvements to the subgrade can enhance its elastic modulus, which helps minimize rutting issues.
From the analysis of Figures 14-16, it is recommended that the Asphalt Institute Method be preferred for planning purposes, as it yields more critical results, making the planning process safer compared to The Bina Marga 2017 Method. The Asphalt Institute Method is preferable because it produces more conservative results. Specifically, conservative results in pavement design are critical for ensuring structural reliability, especially under conditions of traffic growth, environmental variability, and material inconsistencies that are often underestimated during the design phase. The Asphalt Institute Method’s conservative predictions provide a higher margin of safety, aligning with best practices in risk management and infrastructure sustainability. This is particularly important for projects with limited maintenance budgets or in regions where early pavement distress could have significant economic and operational impacts.
4 Conclusions
Based on this research, we can draw the following conclusions:
1. Fatigue life of flexible pavement decreases as the elastic modulus of the pavement layer decreases. This is evident when calculating fatigue life using The Bina Marga 2017 Method and The Asphalt Institute Method. Fatigue life calculated with The Bina Marga 2017 Method yields a higher compared to calculations made using The Asphalt Institute Method.
2. Rutting life of flexible pavement also decreases when the elastic modulus of the flexible pavement layer declines. This relationship is evident when calculating rutting life using both The Bina Marga 2017 Method and The Asphalt Institute Method. Rutting life calculated with The Bina Marga 2017 Method yields also higher compared to those derived from The Asphalt Institute Method.
3. Remaining life due to fatigue and rutting, calculated using The Bina Marga 2017 Method, tends to decrease as the elastic modulus of the flexible pavement layer decreases.
4. Remaining life due to fatigue and rutting, calculated using The Asphalt Institute Method, tends to decrease as the elastic modulus of the flexible pavement layer decreases.
5. The remaining life due to fatigue and rutting at all values of elastic modulus is higher using The Bina Marga 2017 Method compared to The Asphalt Institute Method. Therefore, it is recommended to use The Asphalt Institute Method for planning, as it provides more critical results, ensuring that the planning is safer than when using The Bina Marga 2017 Method.
Acknowledgements
The Authors gratefully acknowledge to Direktorat Riset Teknologi dan Pengabdian kepada Masyarakat (DRTPM) Kemdikbudristek for Research Funding of Penelitian Fundamental DRTPM 2024 Scheme, under Contract Number 108/E5/PG.02.00.PL/2024.
References
- Raza, M.S., dan Sharma, S.K. (2024). A review of mechanical and durability properties and microstructure of semi-flexible pavement. Innovative Infrastructure Solutions, 9 (4), art. no. 83. doi: 10.1007/s41062-024-01393-w.
- Khurshid, A., Khan, R., Khan, D., Jamal, H., Hasan, M.R.M., Khedher, K.M., and Salem, M.A. (2024). Micromechanical modeling for analyzing non-linear behavior of flexible pavements under truck loading. Case Studies in Construction Materials, 20, art. no. e02754. doi: 10.1016/j.cscm.2023.e02754.
- Harnaeni, S.R., Hijra, F., Benina, D.A., Utomo, B., Sunarjono, S., Riyanto, A,. Abdurrohim, M., Ayob, A., Nik Azizan, N.A. (2022). Utilization of Concrete Waste as the Substitute for Coarse Aggregates in Asphalt Mixtures. Civil Engineering and Architecture, 10(6), 2396 - 2409. doi: 10.13189/cea.2022.100613.
- Harnaeni, S.R, Pramesti, F.P, Budiarto, A., Setyawan, A., Khan, M.I., Sutanto, M.H. (2020). Study on Structural Performance of Asphalt Concrete and Hot Rolled Sheet Through Viscoelastic Characterization. Materials. 2020; 13(5):1133. doi: 10.3390/ma 13051133.
- A. Riyanto and R.D. Prasetya, “Effect of Fly Ash Filler Levels in the AC-WC Mixture with Takisung Beach Sand as Fine Aggregate in Terms of Unevenness and Marshall Properties”. Dinamika Teknik Sipil. 2020; 13(2).
- M. Solikin. Analysis of 1:1 Fly Ash Type F and Slag Combination in Geopolymer Concrete using Na2SiO3 and NaOH as Alkaline Activator: A Literature Study. Dinamika Teknik Sipil. 2021; 14(1).
- S. Trinugroho. Analysis of the Effect of Additional Materials of Briquette Charcoal Powder and Bestmittel on the Compression Strength of Concrete. Dinamika Teknik Sipil. 2021; 14(2).
- Kumar, B. V. Kiran and Prasad, N. Shiva. (2024). A Study on Flexural Fatigue Performance of Cement-Treated Base in Flexible Pavements Due to Repetitive Loading. Lecture Notes in Civil Engineering, 449, pp. 401-414, doi: 10.1007/978-981-99-8505-0_37.
- Yu, M., and He, T., Xu, K., Cheng, H. and Ren, M. (2023). Structural layer applicability of semi-flexible material for rutting resistance: A coupled temperature-mechanical approach. PLoS ONE, 18 (11 November), art. no. e0294659. doi: 10.1371/journal.pone.0294659.
- Li, L., Guo, E., Lin, Y. and He, Z. (2023). A Design Method on Durable Asphalt Pavement of Flexible Base on Anti-Rutting Performance and Its Application. Materials, 16 (22), art. no. 7122. doi: 10.3390/ma16227122.
- Reddy, D.S.R., Reddy, K.S. (2023). Fatigue Cracking Susceptibility of Cement Grouted Bituminous (CGB) Mix Layers. Arabian Journal for Science and Engineering, 48 (10), pp. 14237-14249. doi: 10.1007/s13369-023-07943-1.
- Ghanizadeh, A.R., Salehi, M., and Jalali, F. Investigating the Effect of Lime Stabilization of Subgrade on the Fatigue & Rutting Lives of Flexible Pavements Using the Nonlinear Mechanistic-Empirical Analysis. (2023). Geotechnical and Geological Engineering, 41 (2), pp. 1287-1307. doi: 10.1007/s10706-022-02336-x.
- Salini, U. and Koshy, S.A. (2023). Dynamic Complex Modulus and Rutting Characteristics of Reclaimed Asphalt Pavement (RAP) Mixes. Lecture Notes in Civil Engineering, 354 LNCE, pp. 311-322. doi: 10.1007/978-981-99-3142-2_25.
- Mutyala, P., Souliman, M.I., and Loganathan, K. (2023). Quantifying the Influence of Geosynthetics on Pavement Performance against Rutting. Airfield and Highway Pavements 2023: Design, Construction, Condition Evaluation, and Management of Pavements - Selected Papers from the International Airfield and Highway Pavements Conference 2023, 1, pp. 406-415. doi: 10.1061/9780784484890.037.
- Zarei, S. and Alae, M., Ouyang, J., and Zhao, Y. (2022). Rutting and surface-initiated cracking mechanisms of semi-flexible pavements with cement asphalt emulsion pastes. International Journal of Pavement Engineering, 24 (2), art. no. 2024187, doi: 10.1080/10298436.2021.2024187.
- Ren, J. and Xu, Y., Zhao, Z., Chen, J., Cheng, Y., Huang, J., Yang, C., and Wang, J. (2022). Fatigue prediction of semi-flexible composite mixture based on damage evolution. Construction and Building Materials, 318, art. no. 126004. doi: 10.1016/j.conbuildmat.2021.126004.
- Sivaprakash, G., Karna, A., Rayudu, Y., and Jillella, B. (2022). Fatigue life analysis of bituminous pavement for different material properties and axle configurations. Materials Today: Proceedings, 68, pp. 2355-2361, doi: 10.1016/j.matpr.2022.09.102.
- Hatoum, A.A, Khatib, J.M., Barraj, F., and Elkordi, A. (2022). Survival Analysis for Asphalt Pavement Performance and Assessment of Various Factors Affecting Fatigue Cracking Based on LTPP Data. Sustainability. 14(19):12408. doi: 10.3390/su141912408.
- Wang, S., Huanyun, Z., Xianhua, C., Minghui, G., Jinxiang, H., and Xincheng, S. (2021). "Fatigue Resistance and Cracking Mechanism of Semi-Flexible Pavement Mixture" Materials 14, no. 18: 5277. doi: 10.3390/ma14185277.
- Wen, Y., Guo, N., Wang, L., Jin, X., Li, W., and Wen, H. (2021). Assessment of various fatigue life indicators and fatigue properties of rock asphalt composite, Construction and Building Materials, Volume 289, doi: 10.1016/j.conbuildmat.2021.123147.
- Nalbandian, K.M., and González, A. (2021). Assessment of self-healing asphalt pavement fatigue life using analytical Jc approach and laboratory results. Construction and Building Materials, Volume 304, doi: 10.1016/j.conbuildmat.2021.124623.
- De Oliveira, L.S., Babadopulos, L.F.D.A.L., and Soares, J.B. (2021). Evolution of asphalt binder stiffness during fatigue loading and rest periods and its impact on fatigue life, International Journal of Fatigue, Volume 144, doi: 10.1016/j.ijfatigue.2020.106041.
- Chen, Hui and Bahia, Hussain U. (2021). Modelling effects of aging on asphalt binder fatigue using complex modulus and the LAS test. International Journal of Fatigue, 146, art. no. 106150. doi: 10.1016/j.ijfatigue.2021.106150.
- Ziari, H., Amini, A., and Goli, A. (2020). The effect of different aging conditions and strain levels on relationship between fatigue life of asphalt binders and mixtures, Construction and Building Materials, Volume 244, doi: 10.1016/j.conbuildmat.2020.118345.
- Xu, X.Q., Yang, X., Yang, W., Guo, X.G., and Xiang, H.L. (2020). New damage evolution law for modeling fatigue life of asphalt concrete surfacing of long-span steel bridge, Construction and Building Materials, Volume 259, doi: 10.1016/j.conbuildmat.2020.119795.
- Fang, C., Guo, N., You, Z., and Tan, Y. (2020). Investigating fatigue life prediction of rubber asphalt mixture based on damage evolution using residual strain analysis approach, Construction and Building Materials, Volume 257, doi: 10.1016/j.conbuildmat.2020.119476.
- Gong, M., Xiong, Z., Chen, H., Deng, C., Chen, X., Yang, J., Zhu, H., and Hong, J. (2019). Evaluation on the cracking resistance of semi-flexible pavement mixture by laboratory research and field validation. Construction and Building Materials, 207, pp. 387-395. doi: 10.1016/j.conbuildmat.2019.02.064.
- Hamdi, A. (2023). Effect of temperature on service life of flexible pavement using finite element analysis. Geomechanics and Engineering, 32 (5), pp. 513-521. doi: 10.12989/gae.2023.32.5.513.
- Morovatdar, A., Ashtiani, R.S., and Mahmoud, E. (2023). Mechanistic approach to predict service life of flexible pavements subjected to heavy traffic loads. Road Materials and Pavement Design, 24 (2), pp. 427-446, doi: 10.1080/14680629.2021.2019092.
- Isradi, M., Prasetijo, J., Prasetyo, Y.D., Hartatik, N., and Rifai, A.I. (2023). PREDICTION OF SERVICE LIFE BASE ON RELATIONSHIP BETWEEN PSI AND IRI FOR FLEXIBLE PAVEMENT. Proceedings on Engineering Sciences, 5 (2), pp. 267-274. doi: 10.24874/PES05.02.009.
- Adiyasa, M. (2021). ANALYSIS OF REMAINING SERVICE LIFE FOR FLEXIBLE PAVEMENT USING MECHANISTIC-EMPIRICAL METHODS. International Journal of GEOMATE, 21 (85), pp. 145-153. doi: 10.21660/2021.85.j2203.
- Nabipour, N., Karballaeezadeh, N., Dineva, A., Mosavi, A., Mohammadzadeh, S. D., and Shamshirband, S. (2019). Comparative Analysis of Machine Learning Models for Prediction of Remaining Service Life of Flexible Pavement. Mathematics. 2019; 7(12):1198. doi: 10.3390/MATH7121198.
- [33] Bina Marga. (2017). “Manual Perkerasan Jalan (Revisi Juni 2017) Nomor : 04/SE/Db/2017”. Jakarta: DPU Dirjen Bina Marga, 2017.
- Huang, Y. H. (2012). Pavement Analysis and Design (Second Edi). Upper Saddle River, New Jersey: Pearson Prentice Hall. Englewood Cliffs. New Jersey, U.S.A
- Haris, I. and Rahmawati, A. (2018). Evaluasi tebal lapis tambah perkerasan lentur menggunakan metode bina marga (pd t-05-2005-b) dan asphalt institute (ms-17) (studi kasus jalan yogyakarta- bantul). Semesta Teknika, 16(2), 166-171. doi: 10.18196/st.v16i2.4909
- Lakawa, I., Syamsuddin, S., Hujiyanto, H., & Alfian, M. (2024). Review of pavement thickness and road damage using an empirical approach. Technium Romanian Journal of Applied Sciences and Technology, 23, 44-53. doi: 10.47577/technium.v23i.11584
- Liu, Z., Gu, X., Ren, H., Li, S., & Dong, Q. (2023). Permanent deformation monitoring and remaining life prediction of asphalt pavement combining full-scale accelerated pavement testing and fem. Structural Control and Health Monitoring, 2023, 1-19. doi: 10.1155/2023/6932621
- Cheng, C., Ye, C., Yang, H., & Wang, L. (2023). Predicting rutting development of pavement with flexible overlay using artificial neural network. Applied Sciences, 13(12), 7064. doi: 10.3390/app13127064
- Isradi, M., Prasetijo, J., Aden, T., & Rifai, A. (2023). Relationship of present serviceability index for flexible and rigid pavement in urban road damage assessment using pavement condition index and international roughness index. E3s Web of Conferences, 429, 03012. doi: 10.1051/e3sconf/202342903012
Conflict of Interest Statement
The authors declare that there are no conflicts of interest that could have influenced the outcomes or interpretation of this research.
Author Contributions
Data Availability Statement
The data supporting the findings of this study are available from the corresponding author upon reasonable request.
Supplementary Materials
No supplementary materials are associated with this study.