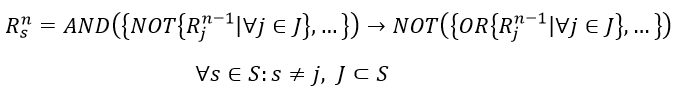Original Scientific Paper, Volume 23, Number 2, Year 2025, No 1281, pp 384-393
Received: Mar 10, 2025 Accepted: Jun 10, 2025 Published: Jun 16, 2025
DOI: 10.5937/jaes0-57515
LOGICAL-STATIC PLANNING COMPLEX TECHNICAL OBJECTS OPERATIONS AND FUNCTIONING MODES
Abstract
A definition of operating mode of complex technical object (CTO) concept is introduced. A logical-static interpretation of CTO operating modes is given. A formal grammar of transformations of logical functions for compatibility (incompatibility) of operations in constraints of a static planning model is presented. Transformation rules are introduced for specific cases. An algorithm for formalizing logical multi-mode structures of CTO functioning in static planning terms of operation flows and modes is developed. Results of computational experiments are presented.
Highlights
- Defined CTO operating mode concept for logical-static planning.
- Developed formal grammar for transforming logical constraints to LP.
- Proposed algorithm for multi-mode CTO operation optimization.
- Validated model with computational experiments on logical operations.
Keywords
Content
1 Introduction
The main elements and subsystems of Industry 4.0 are complex technical objects (CTOs) [1]. Individual computers, computer networks, industrial lines, modern agricultural enterprises, supply chains and networks, etc. are CTOs, which perform many operations [2]. By operation, we mean an action performed by a single functional element (FE) of a CTO [3]. We assume that operations can be performed in parallel or series, with intensity control and the ability to reconfigure the composition of their elements and subsystems (multi-mode).
Based on the studies [4,5], we describe CTO functioning according to the basic provisions of the conceptual model of the functioning of an active mobile object. We suppose that for CTO control and management, it is important not to know its design features but to understand the manifestation of these features. At the same time, the goals of CTO functioning can be achieved in various ways (implementation of aggregated operations (AOs)). In this case, the functioning of the CTO can be described at one of four levels: the level of goals, the level of subgoals, the AO level, or the level of operating modes of subsystems. The CTO operating mode we consider as AO logical interrelations, which performed by various FE to achieve the specified goals. In this paper the aspect of compatibility and incompatibility of the CTO operating modes (described using logical functions), is considered [6].
1.1 Literature review
There is a large body of research focused on using linear programming (LP) methods for planning and scheduling CTO functioning [7,8]. Across a number of decades, this approach has served as the basis for solving specific planning and scheduling tasks in various fields [9].
There is evidence, however, that some CTO operations are linked by logical connections. To illustrate this, researchers have proposed using AND/OR graphs [10,11] to describe the logic of CTO functioning. Drawing on the logical-dynamic description of CTO functioning, researchers have demonstrated that it is possible to create an integrated operational and flow model [12]. The authors have shown that the resulting plans and schedules possess the properties of completeness, closure, and consistency, as they are based on fundamental results from optimal control theory.
The analysis showed that researchers use the principle of decomposition to address the problems of high dimensionality, nonstationary, and nonlinearity [4,13]. Studies have also shown that creating a specific model is a time-consuming process. Firstly, introducing restrictions in optimization planning tasks related to specific operating procedures is always individual in nature, requiring a deep understanding of the subject area. Secondly, for instance, the procedure for forming conjugate variables to solve optimal control problems is quite complicated [14]. At the same time, a number of practical logical constraints cannot be formally described using logical-dynamic models. This means that the creator of the planning model must describe in detail all alternative ways to achieve the goal (technology) [15,16].
As an approach to choosing the composition of operations to ensure the CTO operation modes, the formalization and solution of the optimization problem are proposed. This is because ensuring the specified modes of operation of the CTO involves performing a set of operations that, as a rule, have functional redundancy (variability in the choice of operations to ensure the required mode of operation of the CTO). In particular, the optimization problem can be formalized and solved in terms of a class of LP models. However, at the moment, there is no single procedure for translating logical constraints into the constraints of an LP problem.
To address this gap, we take a rather novel approach. We propose implementing a formal representation of logical functions reflecting the compatibility or incompatibility of the implementation of operating modes in the form of a formal grammar for their transformation into constraints of a static planning model.
1.2 Conceptual statement of the problem
We propose formalizing the logic of implementing operating modes in the form of additional constraints on the time variables for activating the modes under consideration. In this case, the sought variables reflecting the integral time of mode activation must not only satisfy the specified logical conditions of compatibility/incompatibility in mode implementation but also ensure compliance with arbitrarily complex logical relationships between the operating modes and the operations supporting them [17,18]. These relationships are presented in this article in the form of a tree of logical functions.
Let us introduce the following notations:
|
total operating time of a multi-mode CTO – ensuring the implementation of AO; |
|
|
the operating time of the CTO in one of the modes (submodes) at the n-th nesting level of the logical function tree: |
|
|
the operating time of the CTO in the mode (submode) that is ensured by the joint (parallel) execution |
|
|
the operating time of the CTO in the mode (submode) that is ensured by the joint (parallel-sequential) execution |
|
|
the operating time of the CTO, during which the execution of specified operations is prohibited, where s is the number |
2 Materials and methods
2.1 Formal grammar of logical functions transformation of aggregate operation interconnections into constraints of linear programming problem
The process of transforming logical functions into constraints of the LP problem can be represented in the form of the following formal grammar:
|
|
(1) |
where:
S - the CTO operating mode, ensuring the implementation of AO;
N - set of logical operations that characterize the relations between the modes and operations of the CTO functioning;
T - restrictions of the LP problem;
F - rules for transforming logical operations into constraints of the LP problem.
To specify the process of transforming logical functions into LP problem constraints, we define the elements of the sets described above.
As is known, the description of any logical function can be carried out with the presence of the operations "AND" (AND, &), "OR" (OR, |), "NOT" (NOT, ~) [19]. Let us introduce these logical relationships between the operating modes and the operations that provide them in the form of the following LP tasks:
- the task of parallel execution of operations, the total time of such an operating mode $R_{s\mathrm{AND}}^n$ can be introduced into the system of constraints as the lower bound of the total time of joint (simultaneous or parallel) execution of operations xi [20]:
| (2) |
where I is a set of indices of submodes and operations that ensure the execution of the mode (submode) $R_{s\mathrm{AND}}^n$;
- the task of non-execution (prohibition of execution) of operations and submodes, in which incompatibility with specified operations and submodes must be ensured over time:
| (3) |
where is the time horizon for planning the operation of the CTO as a whole;
- the problem of parallel-sequential execution of operations and submodes, the total time of activation of $R_{s\mathrm{OR}}^n$ which can be introduced into the system of constraints both as the sum of the execution time of incompatible operations and submodes xi, and as the lower bound of the execution time of joint operations and submodes xi:
| (4) |
In this case, partial compatibility/incompatibility of the execution of operations and submodes xi is allowed.
Here it is necessary to explain a number of features of the presented models. Firstly, in all three models the inequality sign is deliberately used because when formalizing the general LP task there may be other restrictions interconnected with the modes (submodes) or the operations that provide them, and therefore part of the time resource allocated to the operations and susbmodes xi can be used not only to ensure the execution of a given mode of operation of the CTO, and therefore, the equality sign should be used only when such allocation of resources is prohibited. Secondly, it is recommended to use the mode $R_{s\mathrm{NOT}}^n$ with caution in the case of several operations and submodes xi, as practice has shown, clearly expected results are observed either when using a single such operation, or when using an OR mode as an operation. In the constraints of model (3), the sum of xi can only be used for incompatible operations [21-23]. Thirdly, in subsystem (4), the first constraint is obvious (indeed, the mode $R_{s\mathrm{OR}}^n$ cannot be executed for more than the time of incompatible operations and submodes), while the lower group of constraints is not redundant. For example, when formalizing a complex mode $R_{s\mathrm{NOT}}^n \left(R_{s\mathrm{OR}}^{n+1}\right) \lor$, it would be necessary to minimize and rewrite the constraints of subsystem (4), then the model $R_{s\mathrm{OR}}^{n+1} \rightarrow \min R_{s\mathrm{OR}}^{n+1}$ becomes the upper limit of the durations of operations and submodes xi.
To formalize an arbitrary mode of operation of the CTO (in the form of an arbitrary logical function) in terms of LP, one must first determine the criterion for selecting the optimal solution, and then construct a system of constraints in the form of equations and inequalities.
Since this paper focuses on the formalization of a single mode of CTO operation, the maximization of the execution time of the mode specified by a certain logical function is proposed as the criterion for selecting a solution. In other words, it is proposed to find a plan that considering the possibility of introducing additional restrictions into the LP problem, ensures the execution of this mode for as long as possible. In this case, it is possible to use the restrictions of models (2)-(4) as restrictions for some submodes (intermediate modes) that ensure the implementation of the mode $R_1^0$ with the sequential addition of constraints of the form (2)-(4) to the structure of the general planning model constraints, and the maximization of the mode $R_1^0$ should indirectly maximize these modes as well, since an arbitrary logical function can be transformed into a hierarchical tree of operations [24]. Such a tree of logical operations can be illustrated using the example of the operation "exclusive OR" (XOR). A variant of such an implementation and the order of tree traversal (classical depth-first traversal) (Fig. 1).
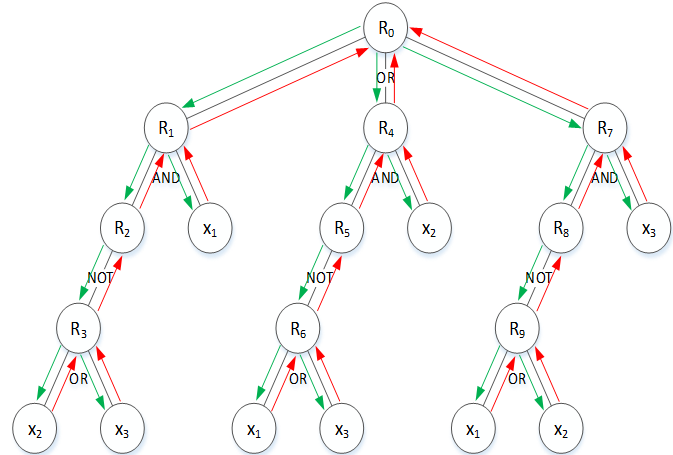
Fig. 1. A variant of a hierarchical tree for the logical operation XOR
In other words, when formalizing the algorithm for parsing the logical function of the mode into a hierarchical tree, an analysis of its components – logical functions and operands – was performed in order to automatically add constraints to the LP model. For the basic logical functions "AND", "OR", "NOT" such constraints are formed (see models (2)-(4), while possible operands require formalization: "SYMBOL" – a symbolic variable (logical variable); constants "TRUE" (true) and "FALSE" (false).
When a symbolic logical variable is found as an operand, the corresponding intermediate mode can be added to the constraint structure of the LP problem as the following expression:
| (5) |
In cases where constants act as operands of a logical function, one of the expressions below should be used:
| (6) | |
| (7) |
It should also be noted that it is impossible to use the introduced transformations directly when implementing complex logical functions of the type $R_{\mathrm{AND}}^n \left( R_{\mathrm{NOT}}^{n+1},\ R_{\mathrm{NOT}}^{n+1} \right)$ and $R_{\mathrm{NOT}}^n \left( R_{\mathrm{AND}}^{n+1} \right)$, since all variables of operations in nested modes will be automatically zeroed. Therefore, according to de Morgan's rules [25], additional transformations of the type (8)-(9) should be implemented:
|
|
(8) |
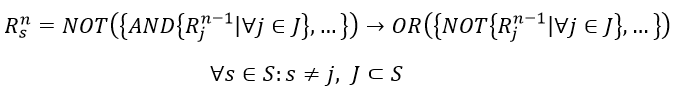 |
(9) |
Thus, if we take constraints (2)-(4) as a basis, take into account additional transformations (5)-(7), (8)-(9) and use submodes instead of operations xi as operands of logical function $R_j^n$s, then the formal grammar of transformations of logical operations of an arbitrary logical function into constraints of the LP problem will finally take the following form [26], were
S is a set of mode (sub-modes) numbers, formed dynamically when traversing the operation tree;
J - a set of submode numbers included in the set of operands of logical functions;
I - a set of numbers of logical variables;
n - the number of the current nesting level of the operations tree.
| (10) | |
 |
|
| (11) | |
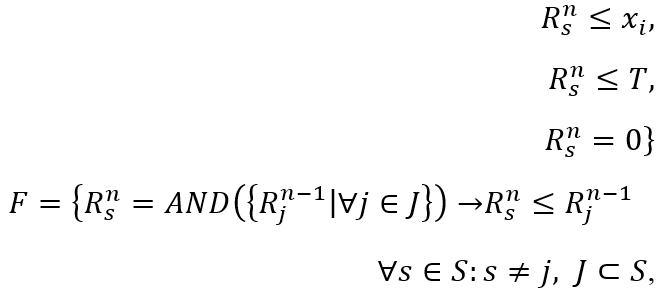 |
|
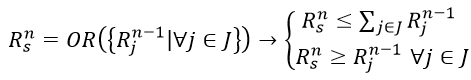 |
(12) |
| (13) |
 |
2.2 Algorithm for transforming logical operations of an arbitrary logical function into constraints of a linear programming problem
Based on the transformation model presented above, an algorithm was developed, the central link of which is a recursive traversal of the tree of logical operations, at each step of which the following occurs:
- adding a new constraint to the structure of the LP task depending on the type of logical operation and operands;
- updating the set by adding the next index number.
After completing the traversal of the logical operation tree, it is necessary to add a group of restrictions on the permissible activation time:
| (14) |
The general scheme of the algorithm is presented in (Fig. 2 – 3).

Fig. 2. Scheme of the algorithm for recursive transformation of a logical function into a structure of constraints of a linear programming problem
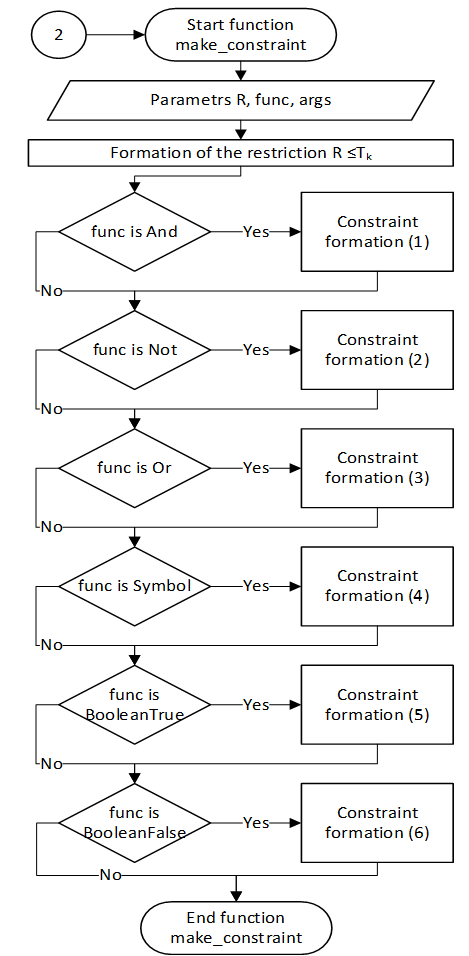
Fig. 3. Scheme of the algorithm for recursive transformation of a logical function into the structure of constraints of a linear programming problem
3 Results and discussion
Based on the developed algorithm, computational experiments were conducted, including checking the implementation of the main properties of logical operations, three variants of implementing XOR and several other examples of logical operations [27,28]. For all the experiments, the time resource. Tk=1. Let us analyze the simulation results presented in Table 1. Here, the variables are operations, and are modes Ri (submodes) at the corresponding nesting levels.
Table 1. Simulation results
| No. | Logical expression | Operation tree in text form | Dimensionality of the LP problem | Solution results (non-zero variables) |
| 1. | (p1 & ~ (p2 | p3)) | (p2 & ~ (p1 | p3)) | (p3 & ~ (p1 | p2)) | R3 Or [p2, p3]R2 Not [R3]R1 And [p1, R2]R6 Or [p1, p3]R5 Not [R6]R4 And [p2, R5]R9 Or [p1, p2]R8 Not [R9]R7 And [p3, R8]R0 Or [R1, R4, R7] | 13 x 35 | R0: 1.0,R1: 0.333, R2: 0.333,R3: 0.333, R4: 0.333,R5: 0.333, R6: 0.333,R7: 0.333, R8: 0.333,R9: 0.333, p1: 0.333,p2: 0.333,p3: 0.333 |
| 2 | (p1 & ~p2 & ~p3) | (p2 & ~p1 & ~p3) | (p3 & ~p1 & ~p2) | R2 Not [p2]R3 Not [p3]R1 And [p1, R2, R3]R5 Not [p1]R3 Not [p3]R4 And [p2, R5, R3]R5 Not [p1]R2 Not [p2]R6 And [p3, R5, R2]R0 Or [R1, R4, R6] | 10 x 41 | R0: 1.0,R1: 0.333, R2: 0.333,R3: 0.333, R4: 0.333,R5: 0.333, R6: 0.333, p1: 0.333,p2: 0.333,p3: 0.333 |
| 3. | (p1 | p2 | p3) & (~p1 | ~p2) & (~p1 | ~p3) & (~p2 | ~p3) | R1 Or [p1, p2, p3]R3 Not [p1]R4 Not [p2]R2 Or [R3, R4]R3 Not [p1]R6 Not [p3]R5 Or [R3, R6]R4 Not [p2]R6 Not [p3]R7 Or [R4, R6]R0 And [R1, R2, R5, R7] | 11 x 37 | R0: 1.0, R1: 1.0,R2: 1.0, R3: 0.5,R4: 0.5, R5: 1.0,R6: 0.5, R7: 1.0, p1: 0.5,p2: 0.5 |
| 4. | p1 | ~p1 | R2 Not [R1]R0 Or [R1, R2] | 5 x 8 | R0: 1.0, R2: 1.0 |
| 5. | p1 & ~p1 | R2 Not [R1]R0 And [R1, R2] | 5 x 7 | R0: 0.5, R1: 0.5, R2: 0.5 |
| 6. | p1 & False | - | 3 x 4 | - |
| 7. | p1 | False | R0 Symbol p1 | 4 x 4 | R0: 1.0, p1: 1.0 |
| 8. | ~p1 | R0 Not [R1] | 4 x 4 | R0: 1.0 |
| 9. | p1 | p2 | p3 | R0 Or [p1, p2, p3] | 4 x 8 | R0: 1.0, p1: 1.0 |
| 10. | p1 & p2 & p3 | R0 And [p1, p2, p3] | 4 x 10 | R0: 1.0, p1: 1.0,p2: 1.0, p3: 1.0 |
| 11. | p1 & (p2 | p3) | R1 Or [p2, p3]R0 And [p1, R1] | 5 x 12 | R0: 1.0, R1: 1.0,p1: 1.0, p2: 1.0, |
| 12. | ((p4 & ~p5) | (p5 & ~p4)) & ((p1 & ~ (p2 | p3)) | (p2 & ~ (p1 | p3)) | (p3 & ~ (p1 | p2))) | R3 Not [p5]R2 And [p4, R3]R5 Not [p4]R4 And [p5, R5]R1 Or [R2, R4]R9 Or [p2, p3]R8 Not [R9]R7 And [p1, R8]R12 Or [p1, p3]R11 Not [R12]R10 And [p2, R11]R15 Or [p1, p2]R14 Not [R15]R13 And [p3, R14]R6 Or [R7, R10, R13]R0 And [R1, R6] | 21 x 66 | R0: 1.0, R1: 1.0,R10: 0.333, R11: 0.333,R12: 0.333, R13: 0.333,R14: 0.333, R15: 0.333,R4: 1.0, R5: 1.0,R6: 1.0, R7: 0.333,R8: 0.333, R9: 0.333, p1: 0.333,p2: 0.333,p3: 0.333,p5: 1.0 |
| 13. | p2 | ~p1 | R1 Not [p1]R0 Or [p2, R1] | 4 x 8 | R0: 1.0, R1: 1.0 |
| 14. | p2 & ~p1 | R1 Not [p1]R0 And [p2, R1] | 4 x 7 | R0: 1.0, R1: 1.0,p2: 1.0 |
| 15. | ~ (p1 & p2 & p3) | R1 And [p1, p2, p3]R0 Not [R1] | 5 x 12 | R0: 1.0,p1: 1.0, p2: 1.0, p3: 1.0 |
| 16. | ~ (p1 | p2 | p3) | R1 Or [p1, p2, p3]R0 Not [R1] | 5 x 10 | R0: 1.0 |
Rows 1–3 in Table 1 contain three implementations of the XOR operation. Rows 4–8 are checks for basic logical constructions. Rows 9–16 contain calculations related to various classical logical functions of several arguments. For example, in row 12, the execution of a given mode must be ensured by two simultaneous operations, one of which must be chosen (for any instant of time) as either p4 or p5, and the other as one of p1, p2, p3.
Table 2 shows the verification calculations of three XOR implementations, to which additional constraints of the following type have been added.
Table 2. Verification calculations
|
No. |
Logical expression |
Operation tree in text form |
Dimensionality of the LP problem |
Solution results (non-zero variables) |
|
1. |
(p1 & ~ (p2 | p3)) | (p2 & ~ (p1 | p3)) | (p3 & ~ (p1 | p2)) |
R3 Or [p2, p3]R2 Not [R3]R1 And [p1, R2]R6 Or [p1, p3]R5 Not [R6]R4 And [p2, R5]R9 Or [p1, p2]R8 Not [R9]R7 And [p3, R8]R0 Or [R1, R4, R7] |
16 x 37 |
R0: 1.0, R1: 0.57142857,R2: 0.57142857, R3: 0.28571429,R4: 0.28571429, R5: 0.28571429,R6: 0.57142857, R7: 0.14285714,R8: 0.14285714, R9: 0.57142857, p1: 0.57142857,p2: 0.28571429,p3: 0.14285714c |
|
2. |
(p1 & ~p2 & ~p3) | (p2 & ~p1 & ~p3) | (p3 & ~p1 & ~p2) |
R2 Not [p2]R3 Not [p3]R1 And [p1, R2, R3]R5 Not [p1]R3 Not [p3]R4 And [p2, R5, R3]R5 Not [p1]R2 Not [p2]R6 And [p3, R5, R2]R0 Or [R1, R4, R6] |
13 x 34 |
R0: 1.0,R1: 0.57142857, R2: 0.57142857,R3: 0.57142857, R4: 0.28571429,R5: 0.28571429, R6: 0.14285714, p1: 0.57142857,p2: 0.28571429,p3: 0.14285714 |
|
3. |
(p1 | p2 | p3) & (~p1 | ~p2) & (~p1 | ~p3) & (~p2 | ~p3) |
R1 Or [p1, p2, p3]R3 Not [p1]R4 Not [p2]R2 Or [R3, R4]R3 Not [p1]R6 Not [p3]R5 Or [R3, R6]R4 Not [p2]R6 Not [p3]R7 Or [R4, R6]R0 And [R1, R2, R5, R7] |
14 x 39 |
R0: 1.0, R1: 1.0,R2: 1.0, R3: 0.42857143,R4: 0.57142857, R5: 1.0,R6: 0.57142857, R7: 1.0, p1: 0.57142857,p2: 0.28571429,p3: 0.14285714 |
3.1 Discussion
The calculations presented in Tables 1 and 2 indicate the reliability of the formalization of the proposed grammar for transforming logical constraints on the compatibility/incompatibility of operations and modes into constraints of the static model of operations planning. In particular, in all three cases given in Table 2, the variables p1, p2, p3 have the same values, such that both the requirements for the limited total time of operations and the additional requirements for the relationship between these variables are satisfied [29,30]. The results confirm the adequacy of the proposed formal grammar of transformations of logical functions.
4 Conclusions
In the course of the research, the authors introduced a generalized definition of the concept of "operating mode" of the CTO, which served as the basis for the development of a formal grammar for transforming logical constraints on the compatibility/incompatibility of operations and submodes into constraints of the static planning model (LP). An algorithm for formalizing logical multi-mode structures of the CTO functioning in terms of LP was developed and used to verify the correctness of the research results.
It is advisable to devote further research on this topic to the integration of the resulting constraints: into planning tasks involving dynamically changing structures of information, material and energy flows processing, transmission and storage systems; into planning tasks when making decisions on using resources to perform operations in time slices; into tasks for synthesizing the technical appearance of multimode objects (including agro-biological objects) during their design and optimization of their structures and business processes.
Acknowledgements
The study was funded by the Russian Science Foundation (project No. 24-19-00823), https://rscf.ru/project/24-19-00823/.
References
- Pereira, A. C., Romero, F. (2017). A review of the meanings and the implications of the Industry 4.0 concept. Procedia Manufacturing, vol. 13, 1206-1214, DOI: 10.1016/j.promfg.2017.09.032.
- Zakharov, V. (2022). Combined optimization algorithm of complex technical object functioning and its information system modernization. In Y. S. Vasiliev, N. D. Pankratova, V. N. Volkova, O. D. Shipunova, & N. N. Lyabakh (Eds.), System analysis in engineering and control (pp. 487-497). Springer. DOI:10.1007/978-3-030-98832-6_43.
- Pavlov, A., Pavlov, D., Zakharov, V. (2019). Possible ways of assessing the resilience of supply chain networks in conditions of unpredictable disruptions. IFAC-PapersOnLine, vol. 52, no. 13, 1283-1288, DOI: 10.1016/j.ifacol.2019.11.375.
- Sokolov, B., Ushakov, V., Zakharov, V. (2024). Optimal planning and scheduling of information processes during interaction among mobile objects. International Journal of Production Research, vol. 62, no. 16, 1-20, DOI: 10.1080/00207543.2024.2302388 .
- Sokolov, B. V., Potryasaev, S. A., Korableva, O. N., Zakharov, V. (2022). Methodology support and algorithms for dynamic synthesis of technologies and programs for proactive management of information processes in the industrial internet under a crisis. International Journal of Risk Assessment and Management, vol. 25, no. 3/4, 194, DOI: 10.1504/IJRAM.2022.130524.
- Pavlov, A., Pavlov, D., Umarov, A., Gordeev, A. (2022). Method of structural-parametric synthesis of configuration multi-mode object. Informatics and Automation, vol. 21, no. 4, 812-845, DOI: 10.15622/ia.21.4.7.
- Dantzig, G.B. (1956). Recent advances in linear programming. Management Science, vol. 2, no. 2, 131-144, DOI: 10.1287/mnsc.2.2.131.
- Shapiro, J. F. (1993). Mathematical programming models and methods for production planning and scheduling. In Handbooks in Operations Research and Management Science (Vol. 4, pp. 371-443). Elsevier. DOI: 10.1016/S0927-0507(05)80188-4.
- Ivanov, D., Sokolov, B., Dolgui, A. (2020). Introduction to scheduling in industry 4.0 and cloud manufacturing systems. In D. Ivanov, B. Sokolov, & A. Dolgui (Eds.), Scheduling in Industry 4.0 and Cloud Manufacturing (pp. 1-9). Springer. DOI: 10.1007/978-3-030-43177-8_1
- Milner, B. Z., Evenko, L. I., Rapoport, V. S. (1983). System approach to organization management. Ekonomika.
- Rigney, J. W., Towne, D. M. (1969). Computer techniques for analyzing the microstructure of serial-action work in industry. Human Factors, vol. 11, no. 2, 113-121.
- Ivanov, D., Sokolov, B., Chen, W., Dolgui, A., Werner, F., Potryasaev, S. (2021). A control approach to scheduling flexibly configurable jobs with dynamic structural-logical constraints. IISE Transactions, vol. 53, no. 1, 21-38, DOI: 10.1080/24725854.2020.1739787.
- Cheng, J., Josipovic, L., Constantinides, G.A., Ienne, P., Wickerson, J. (2022). DASS: Combining dynamic & static scheduling in high-level synthesis. IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems, vol. 41, no. 3, 628-641, DOI: 10.1109/TCAD.2021.3065902.
- Dolgui, A., Ivanov, D., Sethi, S. P., Sokolov, B. (2019). Scheduling in production, supply chain and Industry 4.0 systems by optimal control: Fundamentals, state-of-the-art and applications. International Journal of Production Research, vol. 57, no. 2, 411-432, DOI: 10.1080/00207543.2018.1442948.
- Chernykh D, Steshina L, Petukhov I, Andrianov Y, Velev D. The approach to training logging machinery operators. Journal of Applied Engineering Science, vol. 21, no. 1, 2023, 70–75. DOI: 10.5937/jaes0-38214.
- Steshina, L., Glazyrin, A., Petukhov, I., Velev, D., Zlateva, P. (2023). Using convolutional neural networks for training forest machine operators. Studies in Systems, Decision and Control, vol. 457, 555–574, DOI: 10.1007/978-3-031-22938-1_38.
- Gumerov, H. S., Kulikov, G. G., Rizvanov, K. A. (2022). Formation of semantic and logical constraints of the subject area determined by the object, subject and purpose of research. Bulletin of Ufa State Aviation Technical University, vol. 26, no. 3, 138-145, DOI: 10.54708/19926502_2022_26397138.
- Belishkina, T. A., Konstantinova, T. Yu., Lykov, A. A., Markov, D., Mikado, E. N., Sokolov, V. B. (2024). Formalization of transition from IDEF0-diagram to the GPSS-model of life cycle stages of railway automation and remote control systems. Transport Automation Research, vol. 10, no. 2, 368-376, DOI: 10.20295/2412-9186-2023-9-04-368-376.
- Yablonsky, S. V. (1989). Introduction to discrete mathematics. Mir Publishers.
- Levitin, E. S., Polyak, B. T. (1966). Constrained minimization methods. USSR Computational Mathematics and Mathematical Physics, vol. 6, no. 5, 1–50, DOI: 10.1016/0041-5553(66)90114-5.
- Krotov, K. V. (2024). Models of mixed integer linear programming for optimizing the inclusion of tasks in packages and the order of operations with them in pipeline systems. Informatsionno-upravliaiushchie sistemy [Information and Control Systems], no. 6, 46-57, DOI: 10.31799/1684-8853-2024-6-46-57.
- Kibzun, A. I., Rasskazova, V. (2023). Linear integer programming model as mathematical ware for an optimal flow production planning system at operational scheduling stage. Automation and Remote Control, vol. 84, 529-542, DOI: 10.1134/S0005117923050065.
- Shashkin, A. I., Ledenev, M. Y., Shishov, M. M. (2024). About some methods for solving fuzzy linear programming problems. Proceedings of Voronezh State University. Series: Systems Analysis and Information Technologies, no. 4, 43-57, DOI: 10.17308/sait/1995-5499/2023/4/43-57.
- Shetty, P., Singh, S. (2021). Hierarchical clustering: A survey. International Journal of Applied Research, vol. 7, no. 4, 178-181, DOI: 10.22271/allresearch.2021.v7.i4c.8484.
- Copi, I. M., Cohen, C., McMahon, K. (2016). Introduction to logic. Routledge.
- Bresnan, J. (2021). Formal grammar, usage probabilities, and auxiliary contraction. Language, vol. 97, no. 1, 108-150, DOI: 10.1353/lan.2021.0003.
- Gergel, V., Kozinov, E., Barkalov, K. (2021). Computationally efficient approach for solving lexicographic multicriteria optimization problems. Optim Lett, vol. 15, 2469-2495, DOI: 10.1007/s11590-020-01668-y.
- Fahmi, Sh. S., Ponomarev, N. A., Ho, M. T. M. (2023). New operator for outlining railway infrastructure objects. LETI Transactions on Electrical Engineering & Computer Science, vol. 16, no. 9, 70-76, DOI: 10.32603/2071-8985-2023-16-9-70-76.
- Zuenko, A. A., Fridman, O. V. (2024). Developing logical approach to solving automated planning problems: An analytical review. Proceedings of Voronezh State University. Series: Systems Analysis and Information Technologies, no. 4, 104-127, DOI: 10.17308/sait/1995-5499/2023/4/104-127.
- Espolov, T. I., Tireuov, K. M., Bogomolova, I. P., Mizanbekova, S. K. (2021). Development of public-private partnership mechanisms in the grain product sub-complex. Proceedings of the Voronezh State University of Engineering Technologies, vol. 83, no. 2, 277-284, DOI: 10.20914/2310-1202-2021-2-277-284.
Conflict of Interest Statement
The authors declare that there are no conflicts of interest that could have influenced the research or its outcomes.
Author Contributions
Data Availability Statement
No external datasets were generated or analyzed in this study. The simulation code and model parameters not publicly available.
Supplementary Materials
There are no supplementary materials to include.